某小贩每天从批发市场买进一定数量的土豆，其价格为每千克0.60元，卖出的价格是每千克0.80元，卖不掉的土豆可卖给附近的餐厅，不过每千克卖出的价格P（元/千克）与卖出的数量x（千克

Question

某小贩每天从批发市场买进一定数量的土豆，其价格为每千克0.60元，卖出的价格是每千克0.80元，卖不掉的土豆可卖给附近的餐厅，不过每千克卖出的价格P（元/千克）与卖出的数量x（千克）的关系可近似地用图中的一条折线表示．经过市场调查发现，在一个月内（按30天算）有20天每天可卖出100千克，有10天每天只能卖出70千克，而批发市场规定每天批发给小贩的它的数量必须相同．

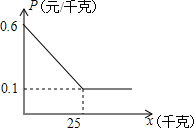
（1）求出价格P（元/千克）与卖给餐厅的土豆数量x（千克）之间的关系式．
（2）设每天小贩从批发市场批发土豆的数量为x（千克），每月所得的毛利润为W（元）．
①根据具体的x（千克）的值，填写下表：

所批发土豆的数量x（千克）	70	90	100
每月所得毛利润W（元）	___	___	___

②该小贩每天从批发市场买进多少千克土豆才能使每月所获得利润最大？最多可赚多少钱？某小贩每天从批发市场买进一定数量的土豆，其价格为每千克0.60元，卖出的价格是每千克0.80元，卖不掉的土豆可卖给附近的餐厅，不过每千克卖出的价格P（元/千克）与卖出的数量x（千克）的关系可近似地用图中的一条折线表示．经过市场调查发现，在一个月内（按30天算）有20天每天可卖出100千克，有10天每天只能卖出70千克，而批发市场规定每天批发给小贩的它的数量必须相同．

（1）求出价格P（元/千克）与卖给餐厅的土豆数量x（千克）之间的关系式．
（2）设每天小贩从批发市场批发土豆的数量为x（千克），每月所得的毛利润为W（元）．
①根据具体的x（千克）的值，填写下表：

所批发土豆的数量x（千克）	70	90	100
每月所得毛利润W（元）	___	___	___

②该小贩每天从批发市场买进多少千克土豆才能使每月所获得利润最大？最多可赚多少钱？

所批发土豆的数量x（千克）	70	90	100
每月所得毛利润W（元）	___	___	___

 所批发土豆的数量x（千克）  70  90  100  每月所得毛利润W（元） ___ ___  ___   所批发土豆的数量x（千克）  70  90  100  所批发土豆的数量x（千克） 70 90 100  每月所得毛利润W（元） ___ ___  ___   每月所得毛利润W（元） ___ ___  ___ 

Answer 1

（1）当0≤x≤25时，设P=kx+b，代入（0，0.6）（25，0.1）得：

b=0.6

25k+b=0.1

，
解得：

k=-0.02

b=0.6

，
∴P=-0.02x+0.6，
当x>25时，P=0.1，
所以P=

-0.02x+0.6(0≤x≤25)

0.1(x>25)

；
（2）①当x=70时，W=（70×0.8-70×0.6）×30=420元，
当x=90时，W=（90×0.8-90×0.6）×20+（70×0.8-70×0.6）×10+20×（-0.02×20+0.6）×10=540元，
当x=100时，W=（100×0.8-100×0.6）×20+（70×0.8-70×0.6）×10+30×0.1×10=570元，
故答案为：420，540，570；
②当x≤70时，W=0.2×x×30=6x，
当x=70时，W最大=420；
当70<x≤95时，W=0.2×x×20+0.2×70×10+（x-70）×[-0.02×（x-70）+0.6]×10=-0.2x²+38x-1260=-0.2（x-95）²+545
当x=95时，W最大=545；
当95<x≤100时，W=0.2×x×20+0.2×70×10+（x-70）×0.1×10=5x+70
当x=100时，W最大=570；
综上所述，x=100时，利润最大为570元．

b=0.6

25k+b=0.1

b=0.6

25k+b=0.1

b=0.6

25k+b=0.1

b=0.6

25k+b=0.1

b=0.6

25k+b=0.1

b=0.625k+b=0.1b=0.6b=0.6b=0.625k+b=0.125k+b=0.125k+b=0.1，
解得：

k=-0.02

b=0.6

，
∴P=-0.02x+0.6，
当x>25时，P=0.1，
所以P=

-0.02x+0.6(0≤x≤25)

0.1(x>25)

；
（2）①当x=70时，W=（70×0.8-70×0.6）×30=420元，
当x=90时，W=（90×0.8-90×0.6）×20+（70×0.8-70×0.6）×10+20×（-0.02×20+0.6）×10=540元，
当x=100时，W=（100×0.8-100×0.6）×20+（70×0.8-70×0.6）×10+30×0.1×10=570元，
故答案为：420，540，570；
②当x≤70时，W=0.2×x×30=6x，
当x=70时，W最大=420；
当70<x≤95时，W=0.2×x×20+0.2×70×10+（x-70）×[-0.02×（x-70）+0.6]×10=-0.2x²+38x-1260=-0.2（x-95）²+545
当x=95时，W最大=545；
当95<x≤100时，W=0.2×x×20+0.2×70×10+（x-70）×0.1×10=5x+70
当x=100时，W最大=570；
综上所述，x=100时，利润最大为570元．

k=-0.02

b=0.6

k=-0.02

b=0.6

k=-0.02

b=0.6

k=-0.02

b=0.6

k=-0.02

b=0.6

k=-0.02b=0.6k=-0.02k=-0.02k=-0.02b=0.6b=0.6b=0.6，
∴P=-0.02x+0.6，
当x>25时，P=0.1，
所以P=

-0.02x+0.6(0≤x≤25)

0.1(x>25)

；
（2）①当x=70时，W=（70×0.8-70×0.6）×30=420元，
当x=90时，W=（90×0.8-90×0.6）×20+（70×0.8-70×0.6）×10+20×（-0.02×20+0.6）×10=540元，
当x=100时，W=（100×0.8-100×0.6）×20+（70×0.8-70×0.6）×10+30×0.1×10=570元，
故答案为：420，540，570；
②当x≤70时，W=0.2×x×30=6x，
当x=70时，W最大=420；
当70<x≤95时，W=0.2×x×20+0.2×70×10+（x-70）×[-0.02×（x-70）+0.6]×10=-0.2x²+38x-1260=-0.2（x-95）²+545
当x=95时，W最大=545；
当95<x≤100时，W=0.2×x×20+0.2×70×10+（x-70）×0.1×10=5x+70
当x=100时，W最大=570；
综上所述，x=100时，利润最大为570元．

-0.02x+0.6(0≤x≤25)

0.1(x>25)

-0.02x+0.6(0≤x≤25)

0.1(x>25)

-0.02x+0.6(0≤x≤25)

0.1(x>25)

-0.02x+0.6(0≤x≤25)

0.1(x>25)

-0.02x+0.6(0≤x≤25)

0.1(x>25)

-0.02x+0.6(0≤x≤25)0.1(x>25)-0.02x+0.6(0≤x≤25)-0.02x+0.6(0≤x≤25)-0.02x+0.6(0≤x≤25)0.1(x>25)0.1(x>25)0.1(x>25)；
（2）①当x=70时，W=（70×0.8-70×0.6）×30=420元，
当x=90时，W=（90×0.8-90×0.6）×20+（70×0.8-70×0.6）×10+20×（-0.02×20+0.6）×10=540元，
当x=100时，W=（100×0.8-100×0.6）×20+（70×0.8-70×0.6）×10+30×0.1×10=570元，
故答案为：420，540，570；
②当x≤70时，W=0.2×x×30=6x，
当x=70时，W最大=420；
当7022+38x-1260=-0.2（x-95）²2+545
当x=95时，W最大=545；
当95当x=100时，W最大=570；
综上所述，x=100时，利润最大为570元．