早教吧作业答案频道 -->数学-->
如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD(1)求证;四边形OBFE是平行四边形;(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?
题目详情
如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD
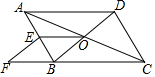
(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD

(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.


(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.如图,在▱ABCD中,对角线AC,BD交于点O,BD交于点O,E为AB中点,点F在CB的延长线上,且EF∥BD

(1)求证;四边形OBFE是平行四边形;
(2)当线段AD和BD之间满足什么条件时,四边形OBFE是矩形?并说明理由;
(3)当线段AD和BD之间满足什么条件时,四边形OBFE是正方形?请画出图形,并说明理由.

▼优质解答
答案和解析
(1)证明:四边形ABCD是平行四边形,
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.
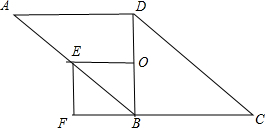
理由:∵OE为△ABD的中位线,
∴OE=
AD
∵O为BD中点,
∴OB=
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
1 2 1 1 12 2 2AD
∵O为BD中点,
∴OB=
BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
1 2 1 1 12 2 2BD,
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
∴OA=OC,
∵E为AB中点,
∴AE=BE
∴OE为△ABC的中位线,
∴OE∥BC,
∵EF∥BD,
∴四边形OBFE是平行四边形.
(2)结论:当AD⊥BD时,四边形OBFE是矩形
∵四边形ABCD是平行四边形,
∴OB=OD
∵E为AB中点,
∴AE=BE
∴OE为△ABD的中位线,
∴OE∥AD,
∴∠BOE=∠BDA,
∵AD⊥BD,
∴∠BOE=BDA=90°,
∵四边形OBFE是平行四边形,
∴四边形OBFE是矩形.
(3)结论:当AD⊥BD AD=BD时,四边形OBFE是正方形.

理由:∵OE为△ABD的中位线,
∴OE=
| 1 |
| 2 |
∵O为BD中点,
∴OB=
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
| 1 |
| 2 |
∵O为BD中点,
∴OB=
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
| 1 |
| 2 |
∵AD=BD,
∴OB=OE,
∵当AD⊥BD时,四边形OBFE是矩形,
∴当AD⊥BD AD=BD时,四边形OBFE是正方形.
看了 如图,在▱ABCD中,对角线...的网友还看了以下:
()是立国之本,是我们党、我们国家生存发展的政治基石.A.党的基本路线B.四项基本原则C.改革开放 2020-04-22 …
在社会主义现代化建设中,我们制定一切方针政策的根本依据是()A.党在社会主义初级阶段的基本路线B. 2020-04-22 …
()是立国之本,是我们党、我们国家生存发展的政治基石.A.党的基本路线B.四项基本原则C.改革开放 2020-04-22 …
给出下列命题:①若向量AB,BC共线,则A,B,C三点共线;②若空间中三个向量共面,则这三个向量的 2020-05-13 …
一个使我困惑的数学概念,若P、A、B、C为空间不同的四点,且有向量PA=a*向量PB+b*向量PC 2020-05-22 …
线性尺寸一般公差规定了()个等级。A.三B.四C.五D.六 2020-06-07 …
已知二次函数y=(x+2)^2的图像与x轴交于点A,于y轴交于点B(1)在对称轴上是否存在一点P, 2020-07-21 …
潜望远镜的问题潜望远镜能观察海面上的物体,说明光是传播的.A.曲线B.四面八方C.直线 2020-11-07 …
读北美局部地区相关信息图,回答下列问题.(1)丙图中②是山系.(2)丙图最可能是沿甲图中哪条线所做的 2020-12-17 …
建设中国特色社会主义的总依据是()A.党的基本路线B.四项基本原则C.马列主义、毛泽东思想D.社会主 2020-12-24 …