早教吧作业答案频道 -->数学-->
已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.(1)如图1,当点F落在BC边上时.①EF+=CD;②△AFB与△FEC有什么关系?说明理由.(2)如图2
题目详情
已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.
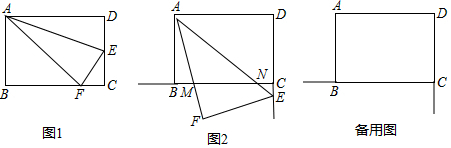
(1)如图1,当点F落在BC边上时.
①EF+___=CD;
②△AFB与△FEC有什么关系?说明理由.
(2)如图2,当点E在DC延长线上时,AF与射线CB交于点M,AE与边BC交于点N,
①当点M在BC边上时,请你判断MB、MF、NC之间有怎样的数量关系?并说明理由;
②当点M在CB延长线时,请你直接写出MB、MF、NC之间的数量关系.
 已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.
已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.
(1)如图1,当点F落在BC边上时.
①EF+___=CD;
②△AFB与△FEC有什么关系?说明理由.
(2)如图2,当点E在DC延长线上时,AF与射线CB交于点M,AE与边BC交于点N,
①当点M在BC边上时,请你判断MB、MF、NC之间有怎样的数量关系?并说明理由;
②当点M在CB延长线时,请你直接写出MB、MF、NC之间的数量关系.


(1)如图1,当点F落在BC边上时.
①EF+___=CD;
②△AFB与△FEC有什么关系?说明理由.
(2)如图2,当点E在DC延长线上时,AF与射线CB交于点M,AE与边BC交于点N,
①当点M在BC边上时,请你判断MB、MF、NC之间有怎样的数量关系?并说明理由;
②当点M在CB延长线时,请你直接写出MB、MF、NC之间的数量关系.
 已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.
已知矩形ABCD中,点E是射线DC上一个动点,将△ADE沿直线AE折叠,得到△AFE,点D的对应点为点F.(1)如图1,当点F落在BC边上时.
①EF+___=CD;
②△AFB与△FEC有什么关系?说明理由.
(2)如图2,当点E在DC延长线上时,AF与射线CB交于点M,AE与边BC交于点N,
①当点M在BC边上时,请你判断MB、MF、NC之间有怎样的数量关系?并说明理由;
②当点M在CB延长线时,请你直接写出MB、MF、NC之间的数量关系.


▼优质解答
答案和解析
(1)如图1中,
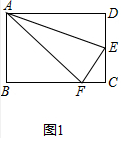
①∵△AEF是由△AED翻折得到,
∴DE=EF,
∵DE+EC=DC,
∴EF+EC=DC,
故答案为EC.
②结论:△AFB∽△FEC.
理由:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,
∴∠AFB=∠EFC,
∴△AFB∽△FEC.
(2)①如图2中,结论:FM=BM+CN.
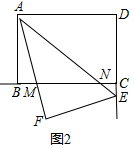
理由:∵△AEF是由△AED翻折得到,
∴∠DAE=∠EAF,AF=AD,
∵AD∥BC,AD=BC,
∴∠DAN=∠ANM,
∴∠MAN=∠MNA,
∴AM=MN,
∴FM+AM=AD=BC,
∴FM+MN=BC,
∵BM+CN+MN=BC,
∴FM=BM+CN.
②如图3中,结论:FM=CN-BM.
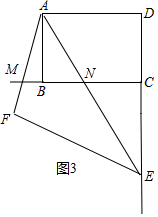
理由:易证FM+MN=BC,MN+CN-BM=BC,
所以FM=CN-BM.

①∵△AEF是由△AED翻折得到,
∴DE=EF,
∵DE+EC=DC,
∴EF+EC=DC,
故答案为EC.
②结论:△AFB∽△FEC.
理由:∵四边形ABCD是矩形,
∴∠B=∠C=90°,
∵∠AFE=90°,
∴∠AFB+∠EFC=90°,∠EFC+∠FEC=90°,
∴∠AFB=∠EFC,
∴△AFB∽△FEC.
(2)①如图2中,结论:FM=BM+CN.

理由:∵△AEF是由△AED翻折得到,
∴∠DAE=∠EAF,AF=AD,
∵AD∥BC,AD=BC,
∴∠DAN=∠ANM,
∴∠MAN=∠MNA,
∴AM=MN,
∴FM+AM=AD=BC,
∴FM+MN=BC,
∵BM+CN+MN=BC,
∴FM=BM+CN.
②如图3中,结论:FM=CN-BM.

理由:易证FM+MN=BC,MN+CN-BM=BC,
所以FM=CN-BM.
看了 已知矩形ABCD中,点E是射...的网友还看了以下:
数学活动:将形状不同的三张矩形纸片按照如图的方式折叠,BE、DF分别是折痕.折叠后点A、C分别落在 2020-04-09 …
如图漫画蕴含的道理是()A.挫折是客观因素导致的B.要直面挫折,战胜挫折C.挫折是人生的宝贵财富D 2020-05-12 …
如图漫画蕴含的道理是()A.挫折是客观因素导致的B.要直面挫折,战胜挫折C.挫折是人生的宝贵财富D 2020-05-12 …
如图漫画告诉我们的道理是()A.挫折的存在具有普遍性,人生难免有挫折B.挫折是人生的宝贵财富,它有 2020-05-15 …
平行于主光轴的光线经折射后过焦点(对凹透镜来说是折射光线的反向延长线过焦点),不太理解,还有↓过焦 2020-05-16 …
那种一吹就亮的“火折子”现实存在吗?原理是什么?就是小说和电视剧中提到的“火折子”,现实中合理吗? 2020-06-02 …
初二物理题1、关于光的反射折射现象下列说法正确的是()a、漫反射是一种折射现象b、平面镜成像是一种 2020-07-22 …
阿基米德折弦定理:如图1,AB和BC是O的两条弦(即折线ABC是圆的一条折弦),BC>AB,M是A 2020-07-30 …
苦难是人生的老师,通过苦难,走向欢乐(德国贝多芬).这句话说明的道理是()A.挫折是一把“双刃剑”, 2020-12-03 …
空间折跃?折跃这个词是怎么出现的?折跃的原理是什么?折跃与时空传送能打等号吗?折跃有可能实现吗? 2020-12-04 …