早教吧作业答案频道 -->数学-->
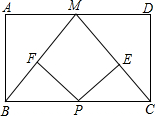
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
题目详情
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
 如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.


 如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.
如图,点M是矩形ABCD的边AD的中点,点P为BC上一点,PE⊥MC于点E,PF⊥MB于点F,当AB,BC满足什么条件时,四边形PEMF为矩形.

▼优质解答
答案和解析
AB=
BC时,四边形PEMF是矩形.
∵在矩形ABCD中,M为AD边的中点,AB=
BC,
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
1 2 1 1 12 2 2BC时,四边形PEMF是矩形.
∵在矩形ABCD中,M为AD边的中点,AB=
BC,
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
1 2 1 1 12 2 2BC,
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
| 1 |
| 2 |
∵在矩形ABCD中,M为AD边的中点,AB=
| 1 |
| 2 |
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
| 1 |
| 2 |
∵在矩形ABCD中,M为AD边的中点,AB=
| 1 |
| 2 |
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
| 1 |
| 2 |
∴AB=DC=AM=MD,∠A=∠D=90°,
∴∠ABM=∠MCD=45°,
∴∠BMC=90°,
又∵PE⊥MC,PF⊥MB,
∴∠PFM=∠PEM=90°,
∴四边形PEMF是矩形.
看了 如图,点M是矩形ABCD的边...的网友还看了以下:
已知M,P是两个不等的非空集合,则必有() A.空集属于M交P B.空集等于M交P,C.空集包含于 2020-05-16 …
关于数学圆锥曲线椭圆的问题已知圆O:x^2+y^2=4 ,从这个圆上任意一点P向y轴作垂线段PP1 2020-06-27 …
设M,P是两个非空集合,定义M与P的差集为M一P={x|x属于M且x不属于P},则M一(M一P)等 2020-07-11 …
M={1,2},求P={X|X属于M}P是不是有四个解啊?P={1,2}或{1}或{2}或空集,还 2020-07-30 …
设M,P是任意两个不等的非空集合,则必有A空集∈(M∩P)B空集=M∩PC(M∩P)包含空集D.( 2020-07-30 …
集合M={x│x=3k-2,k∈Z},集合P={x│x=3l+1,l∈Z},集合S={x│x=6m 2020-08-01 …
设M.P是两个非空集合,定义M-P={xx属于M,且x不属于P},若M={x1小于等于x小于等于2 2020-08-01 …
i几道关于高中的数学题1.若A={a,0,1},B={c+b,1/b+a,1},且A=B,则a=, 2020-08-01 …
已知M,P是两个非空集合,定义M-P=x,且X属于M不属于P,则P-(M-P)=? 2020-08-01 …
设M,P是两个非空集合规定M-P={xlx属于M且x不属于P,则M-(M-P)=? 2020-08-01 …