早教吧作业答案频道 -->数学-->
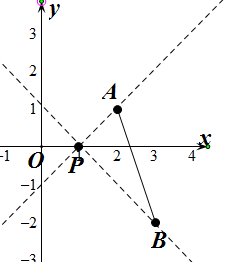
已知直线l经过点P(1,0)且与以A(2,1),B(3,-2)为端点的线段AB有公共点,则直线l的倾斜角的取值范围是.
题目详情
已知直线l经过点P(1,0)且与以A(2,1),B(3,-2)为端点的线段AB有公共点,则直线l的倾斜角的取值范围是___.已知直线l经过点P(1,0)且与以A(2,1),B(3,-2)为端点的线段AB有公共点,则直线l的倾斜角的取值范围是___.
▼优质解答
答案和解析
 ∵kPAPA=
∵kPAPA=
=1,kPB=
=-1.
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
1-0 2-1 1-0 1-0 1-02-1 2-1 2-1=1,kPBPB=
=-1.
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
-2-0 3-1 -2-0 -2-0 -2-03-1 3-1 3-1=-1.
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
 ∵kPAPA=
∵kPAPA=| 1-0 |
| 2-1 |
| -2-0 |
| 3-1 |
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
| 1-0 |
| 2-1 |
| -2-0 |
| 3-1 |
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
| -2-0 |
| 3-1 |
∴直线PA,PB的倾斜角分别为45°,135°.
∵直线l与连接A(2,1),B(3,-2)的线段有公共点,
∴直线l的斜率k满足-1≤k≤1
∴直线l的倾斜角的取值范围是[0,45°]∪[135°,180°).
故答案为:[0,45°]∪[135°,180°).
看了 已知直线l经过点P(1,0)...的网友还看了以下:
直线y=kx+b与直线y=-3x平行,且过点(-3,2)则直线y=kx+b的解析式为直线y=kx+ 2020-05-13 …
在同一平面内,过一点可能有两条以上的直线与已知直线平行吗?任意画一条直线a,在直线外取点P,并过点 2020-06-06 …
同一平面内,直线a与直线b互相垂直,直线c与直线a互相垂直,那么直线b与直c的关系是. 2020-06-15 …
一张白纸上有三条直线,已知直线a平行于直线b,直线b平行于直线c,且直线a与直线b之间的距离为3厘 2020-06-19 …
如图,直线a与直线b被直线c所截,b⊥c,垂足为点A,∠1=70°.若使直线b与直线a平行,则可将 2020-07-22 …
一张白纸上有三条直线,已知直线a平行于直线b,直线b平行于直线c且直线a与直线b之间的距离为3厘米 2020-07-22 …
已知直线y=kx+b与直线y=3x-1/2平行,且过点(2/3,0)(1)求这条直线的表达式(2) 2020-07-23 …
在平面直角坐标系中,坐标原点为O,直线1:y=x+4与x轴交于点A,直线2:y=-x+2与Y轴交于B 2020-11-01 …
如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行 2020-11-03 …
(2014•长春)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°,若使 2020-11-03 …