早教吧作业答案频道 -->数学-->
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且SEEC=SFFD=AGGC.(1)求证:FG∥平面SAB;(2)若平面ABE⊥平面SCD,求多面体SABEF
题目详情
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且
=
=
.
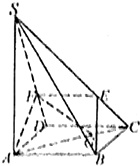
(1)求证:FG∥平面SAB;
(2)若平面ABE⊥平面SCD,求多面体SABEF的体积.
| SE |
| EC |
| SF |
| FD |
| AG |
| GC |

(1)求证:FG∥平面SAB;
(2)若平面ABE⊥平面SCD,求多面体SABEF的体积.
▼优质解答
答案和解析
证明:(1)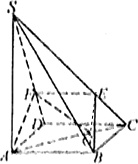 连结EG.
连结EG.
∵
=
,
=
,
∴EG∥SA,EF∥CD,又AB∥CD,
∴EF∥AB,
∵EF⊂平面EFG,EG⊂平面EFG,AB⊂平面SAB,SA⊂平面SAB,EF∩EG=E,SA∩AB=A,
∴平面EFG∥平面SAB.
∵FG⊂平面EFG,
∴FG∥平面SAB.
(2)∵SA⊥平面ABCD,AB⊂平面ABCD,
∴SA⊥AB,又AD⊥AB,AD∩SA=A,SA⊂平面SAD,AD⊂平面SAD,
∴AB⊥平面SAD,
∵EF∥AB,
∴EF⊥平面SAD,
∵SF⊂平面SAD,AF⊂平面SAD,
∴EF⊥AF,EF⊥SF,
∵平面ABE⊥平面SCD,平面ABE∩平面SCD=EF,SF⊂平面SCD,
∴SF⊥平面ABEF.
∵AB=CD=AD=4,∠SDA=60°,
∴DF=2,AF=2
,SD=8,
∴SF=6.
∵
=
=
,
∴EF=3.
∴VS-ABEF=
S梯形ABEF•SF=
×
×(3+4)×2
×6=14
.
 连结EG.
连结EG.∵
| SE |
| EC |
| AG |
| GC |
| SF |
| FD |
| SE |
| EC |
∴EG∥SA,EF∥CD,又AB∥CD,
∴EF∥AB,
∵EF⊂平面EFG,EG⊂平面EFG,AB⊂平面SAB,SA⊂平面SAB,EF∩EG=E,SA∩AB=A,
∴平面EFG∥平面SAB.
∵FG⊂平面EFG,
∴FG∥平面SAB.
(2)∵SA⊥平面ABCD,AB⊂平面ABCD,
∴SA⊥AB,又AD⊥AB,AD∩SA=A,SA⊂平面SAD,AD⊂平面SAD,
∴AB⊥平面SAD,
∵EF∥AB,
∴EF⊥平面SAD,
∵SF⊂平面SAD,AF⊂平面SAD,
∴EF⊥AF,EF⊥SF,
∵平面ABE⊥平面SCD,平面ABE∩平面SCD=EF,SF⊂平面SCD,
∴SF⊥平面ABEF.
∵AB=CD=AD=4,∠SDA=60°,
∴DF=2,AF=2
| 3 |
∴SF=6.
∵
| EF |
| CD |
| SF |
| SD |
| 3 |
| 4 |
∴EF=3.
∴VS-ABEF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
看了 如图所示,四棱锥S-ABCD...的网友还看了以下:
.计算题..急有两个实心圆柱体A和B叠放在一起,并且完全接触(A在B的正中上面),已知AB两个圆柱 2020-04-27 …
FORTRAN90,PRINT'(1X,2I5.4)',A,B中1X和2,是什么意思 2020-05-14 …
从飞机的舷窗向外看,窗口画面里有白云、海岛和海域.这幅画面中,白云占了一半且遮住了海岛的1/4,因 2020-05-16 …
一个三角形中的不等式.s.R.r分别为三角形的面积外接圆半径内接圆半径,求证a^4+b^4+c^4 2020-06-06 …
已知a/(a^2+1)=1/2,求a^2/(a^4+1)的值由a/(a^2+1)=1/2,知a≠0 2020-06-14 …
(a+4)(a+3)=();(a+4)(a-3)=();(a+4)(a+3)=();(a+4)(a 2020-07-09 …
(a+4)(a+3)、(a+4)(a-3)、(a-4)(a+3)、(a-4)(a-3)从上面的计算 2020-07-15 …
一个三棱锥的4个面中,直角三角形最多有()A1B2C3D4我选的是C, 2020-07-16 …
圆B与圆C的面积之和等于圆A面积的5分之4,且圆A中的阴影部分占圆A面积的6分之1,圆B中的阴影部 2020-07-21 …
定义一种新运算:a□b表示a,b中最大的数,如4□5=5;a△b表示a,b中最小的数,如4△5=4; 2020-11-01 …