早教吧作业答案频道 -->数学-->
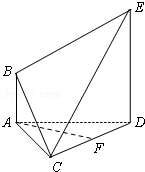
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,BC=5,F是CD的中点.(Ⅰ)求证AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积.
题目详情
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,BC=
,F是CD的中点.
(Ⅰ)求证AF∥平面BCE;
(Ⅱ)求多面体ABCDE的体积.
| 5 |

(Ⅰ)求证AF∥平面BCE;
(Ⅱ)求多面体ABCDE的体积.
▼优质解答
答案和解析
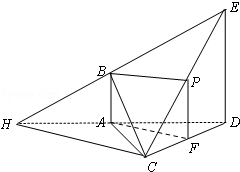
(Ⅰ)证明:取CE中点P,连接FP、BP,
∵F为CD的中点,
∴FP∥DE,且FP=
DE.
又AB∥DE,且AB=
DE.
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP.
又∵AF⊄平面BCE,BP⊂平面BCE,
∴AF∥平面BCE;
(II) ∵直角梯形ABED的面积为
×2=3,C到平面ABDE的距离为
×2=
,
∴四棱锥C-ABDE的体积为V=
×3×
=
.
即多面体ABCDE的体积为
.
∵F为CD的中点,
∴FP∥DE,且FP=
| 1 |
| 2 |
又AB∥DE,且AB=
| 1 |
| 2 |
∴AB∥FP,且AB=FP,
∴ABPF为平行四边形,∴AF∥BP.
又∵AF⊄平面BCE,BP⊂平面BCE,
∴AF∥平面BCE;
(II) ∵直角梯形ABED的面积为
| 1+2 |
| 2 |
| ||
| 2 |
| 3 |
∴四棱锥C-ABDE的体积为V=
| 1 |
| 3 |
| 3 |
| 3 |
即多面体ABCDE的体积为
| 3 |

看了 在如图所示的多面体ABCDE...的网友还看了以下:
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
若a为有理数,则下列说法正确的是A.-a一定是负数B.a的绝对值一定是正数C.-a的绝若a为有理数 2020-06-25 …
在下列四种边长均为a的正多边形中:①正方形;②正五边形;③正六边形;④正八边形;能与边长为a的正三 2020-07-01 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
如图所示,Q带负电荷,导体P在a处接地,下列说法中正确的是()A.导体P的a端带正电荷,b端带负电 2020-07-12 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …