如图，在各棱长均为4的直四棱柱ACCD-A1B1C1D1中，底面ABCD为菱形，∠BAD=60°，E为梭BB1上一点，且BE=3EB1（1）求证：平面ACE丄平面BDD1B1（2）平面AED1将四棱柱ABCD-A1B1C1D1分成上、下两部分．求这两

Question

如图，在各棱长均为4的直四棱柱ACCD-A₁B₁C₁D₁中，底面ABCD为菱形，∠BAD=60°，E为梭BB₁上一点，且BE=3EB₁

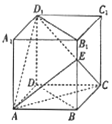
（1）求证：平面ACE丄平面BDD₁B₁
（2）平面AED₁将四棱柱ABCD-A₁B₁C₁D₁分成上、下两部分．求这两部分的休积之比
（梭台的体积公式为V=(1)/(3)（S′+√(SS′)+S）h，其中S'，S分別为上、下底面面积，h为棱台的高）

Answer 1

（1）证明：∵底面ABCD为菱形，∴AC⊥BD，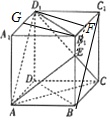
在直四棱柱ACCD-A₁B₁C₁D₁中，∵BB₁⊥底面ABCD，∴BB₁⊥AC，
∵BB₁∩BD=B，∴AC⊥平面BDD₁B₁，
又AC⊂平面ACE，∴平面ACE丄平面BDD₁B₁；
（2） 连接BC₁，过E作EF∥BC₁ 交B₁C₁于F，则B₁F=1，
则平面AED₁ 与侧面BCC₁B₁相交的线段为EF，
故平面AED₁ 将四棱柱ACCD-A₁B₁C₁D₁分成上下两部分．
上部分是三棱台B₁EF-A₁AD₁，取A₁D₁ 的中点G，连接B₁G，
∵底面ABCD为菱形，∠BAD=60°，
∴△ABD为正三角形，即△A₁B₁D₁也为正三角形，
∴B₁G⊥A₁D₁，又AA₁⊥底面A₁B₁C₁D₁，
∴AA₁⊥B₁G，而A₁D₁∩A₁A=A₁，
∴B₁G⊥平面AA₁D₁，
∵S△B1EF=(1)/(2)，S△A1AD1=8，B1G=2√(3)，
∴VB1EF-A1AD1=V上=(1)/(3)×((1)/(2)+2+8)×2√(3)=7√(3)．
又四棱柱ABCD-A₁B₁C₁D₁的体积为32√(3)，
∴V下=32√(3)-V上=25√(3)．
∴(V上)/(V下)=(7)/(25)．