()(本小题满分12分)w.w.w.k.s.5.u.c.o.m如图,直三棱柱ABC-A1B1C1中,AB⊥ACD、E分别为AA1、B1C的中点,DE⊥平面BCC1(Ⅰ)证明:AB=ACw.w.w.k.s.5.u.c.o.m(Ⅱ)
()(本小题满分12分)w.w.w.k.s.5.u.c.o.m ![]()
![]()
如图,直三棱柱ABC-A 1 B 1 C 1 中,AB⊥AC D、E分别为AA 1 、B 1 C的中点,DE⊥平面BCC 1
(Ⅰ)证明:AB=AC w.w.w.k.s.5.u.c.o.m ![]()
![]()
(Ⅱ)设二面角A-BD-C为60° 求B 1 C与平面BCD所成的角的大小
:解法一:(Ⅰ)取BC中点F,连接EF,则EF![]()
![]()
![]() ,从而EF
,从而EF![]() DA.
DA.
连接AF,则ADEF为平行四边形,从而AF//DE.又DE⊥平面![]() ,故AF⊥平面
,故AF⊥平面![]() ,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC.
,从而AF⊥BC,即AF为BC的垂直平分线,所以AB=AC.
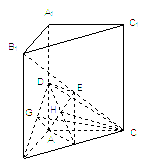 (Ⅱ)作AG⊥BD,垂足为G,连接CG.由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角.由题设知,∠AGC=60 0. .
(Ⅱ)作AG⊥BD,垂足为G,连接CG.由三垂线定理知CG⊥BD,故∠AGC为二面角A-BD-C的平面角.由题设知,∠AGC=60 0. .
设AC=2,则AG=![]() .又AB=2,BC=
.又AB=2,BC=![]() ,故AF=
,故AF=![]() .
.
由![]() 得2AD=
得2AD=![]() ,解得AD=
,解得AD=![]() .
.
故AD=AF.又AD⊥AF,所以四边形ADEF为正方形.
因为BC⊥AF,BC⊥AD,AF∩AD=A,故BC⊥平面DEF,因此平面BCD⊥平面DEF.
连接AE、DF,设AE∩DF=H,则EH⊥DF,EH⊥平面BCD.
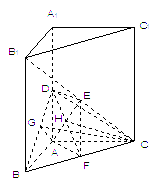 连接CH,则∠ECH为
连接CH,则∠ECH为![]() 与平面BCD所成的角.w.w.w.k.s.5.u.c.o.m
与平面BCD所成的角.w.w.w.k.s.5.u.c.o.m ![]()
![]()
因ADEF为正方形,AD=![]() ,故EH=1,又EC=
,故EH=1,又EC=![]() =2,
=2,
所以∠ECH=30 0 ,即![]() 与平面BCD所成的角为30 0 .
与平面BCD所成的角为30 0 .
解法二:
(Ⅰ)以A为坐标原点,射线AB为x轴的正半轴,建立如图所示的直角坐标系A—xyz.
设B(1,0,0),C(0,b,0),D(0,0,c),则![]() (1,0,2c) E(
(1,0,2c) E(![]() ,
,![]() ,c).
,c).
于是![]() =(
=(![]() ,
,![]() ,0),
,0),![]() =(-1,b 0).由DE⊥平面
=(-1,b 0).由DE⊥平面![]() 知DE⊥BC,
知DE⊥BC, ![]() =0,求得b=1,所以 AB=AC.
=0,求得b=1,所以 AB=AC.
(Ⅱ)设平面BCD的法向量![]() 则
则![]() 又
又![]() =(-1,1,
=(-1,1,
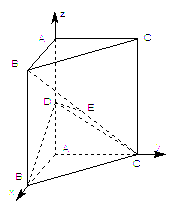
![]() 0),
0),![]() =(-1,0,c) 故
=(-1,0,c) 故
令x=1 则y=1 z=![]()
![]() =(1 1
=(1 1 ![]() ).
).
又平面![]() 的法向量
的法向量![]() =(0,1,0)
=(0,1,0)
由二面角![]() 为60°知,
为60°知,![]() =60°,
=60°,
故 ![]() °,求得
°,求得![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
于是 ![]() ,
, ![]()
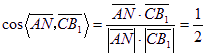 ,
,
![]() °
°
所以![]() 与平面
与平面![]() 所成的角为30°
所成的角为30°
:要证明AB=AC w,,只需证明底边上的中线和底边垂直即可,所以这里要
做辅助线.已知二面角的大小,做题过程要落实,从而找到个棱长的关系,
做二面角的平面角常常利用三垂线定理和逆定理.要证明B 1 C与平面BCD所成
的角,需要找到垂线和垂面.
因为这是一个直棱柱,且AB⊥AC,所以可以建立空间直角坐标系,
利用空间向量证明和求解,常用平面的法向量求线面角.
1.a≠0,b≠0,则a/|a|+b/|b|的不同取值的个数为()A.3B.2C.1D.02.若|x 2020-03-31 …
△ABC三边abc和面积满足S=c2-(a-b)2,且a+b=2△ABC的三边a,b,c和面积S满 2020-04-27 …
读下图,据此回答1-3题:1.四幅图中位在亚洲与北美洲边界的图是:A.a图B.b图C.c图D.d图 2020-05-02 …
基本不等式超费解130已知a>b>0,求a2+1/(a*b)+1/[a*(a-b)]的最小值.a2 2020-05-13 …
设集合A={1,a,b},B={a,a^2,ab}且A=B,求实数A,B的值因为集合需要满足互异性 2020-05-15 …
设集合A={a,b,c,d},A上的二元关系R={,,,}(1)求出r(R),s(R),t(R)( 2020-06-12 …
自动控制原理问题Gs=(s+a)/s(s^2+6s+7)求汇出a从0到无穷的迹,求出使系统稳定且为 2020-06-14 …
在函数y=lgx(x>1)的图像上有M,N,P三点,它们的横坐标分别为a,a+2,a+4,记三角形 2020-06-27 …
假设集合A满足以下条件:诺a∈A,a不等于1,则1-a分之1属于A若a属于A,则1-a分之一属于A 2020-07-03 …
下证明过程中蕴涵的数学思想是什么s=a+a(1+i)+a(1+i)(1+i)+...+a(1+i)的 2020-11-01 …