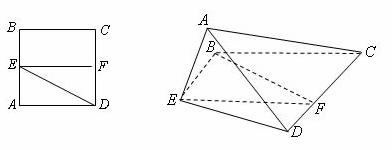
已知正方形ABCD，E，F分别是边AB，CD的中点，将△ADE沿DE折起，如图所示，记二面角A-DE-D的大小为（）．（1）证明BF//平面ADE；（2）若△ACD为正三角形，试判断点A在平面BCDE内的射影

Question

已知正方形ABCD，E，F分别是边AB，CD的中点，将△ADE沿DE折起，如图所示，记二面角A-DE-D的大小为 （ ）．

（1）证明BF//平面ADE；

（2）若△ACD为正三角形，试判断点A在平面BCDE内的射影G是否在直线EF上，证明你的结论，并求角 的余弦值．

Answer 1

（Ⅰ）证明：E、F分别是正方形ABCD的边AB、CD的中点. ∴ED//FB且EB=FD ∴四边形EBFD是平行四边形 ∴BF//ED ∴ED平面AED而BF平面AED ∴BF//平面AED （Ⅱ）解法一：点A在平面BCDE内的射影G在直线EF上，过点A用AG⊥平面BCDE垂足为G，连接GC，GD ∵△ACD为正三角形 ∴AC=AD ∴GC=GD ∴G在CD的垂直平分线上。 又∵EF是CD的垂直平分线 ∴点A在平面BCDE内的射影G在直线EF上 过G作GH⊥ED，垂足为H，连接AH则AH⊥DE ∴∠AHG是二面角A-DE-C的平面角，即∠AHG = 设原正方形ABCD的边长为，连接AF， 在折后图的△AEF中，AF=，EF=2AE= △AEF为直角三角形，AG?EF=AE?AF ∴AG= 在Rt△ADE中，AH?DE=AD?AE ∴AH= ∴GH= ∴ 解法二：点A在平面BCDE内的射影G在直线EF上，连结AF，在平面AEF内过点A作AG′⊥EF，垂足为G′ ∵△ACD为正三角形，F为CD的中点， ∴AF⊥CD 又∵EF⊥CD ∴CD⊥平面AEF ∵AG′平面AEF ∴CD⊥AG′ 又∵AG′⊥EF，且CD∩EF=F，CD平面BCDE，EF平面BCDE， ∴AG⊥平面BCDE， ∴G′为A在平面BCDE内的射影G。 ∴点A在平面BCDE内的射影G在直线EF上 过G作GH⊥ED，垂足为H，连结AH，则AH⊥DE， ∴∠AHG是二面角A-DE-C的平面角，即∠AHG = 设原正方形ABCD的边长为。 在折后图的△AEF中，AF=，EF=2AE= ∴△AEF为直角三角形，AG?EF=AE?AF， ∴AG=， 在Rt△ADE中，AH?DE=AD?AE， ∴AH= ∴GH= ∴ 解法三： 点A在平面BCDE内的射影G在直线EF上连结AF，在平面AEF内过点A作AG′⊥EF，垂足为G′ ∵△ACD为正三角形，F为CD的中点 ∴AF⊥CD 又∵EF⊥CD ∴CD⊥平面AEF ∵CD平面BCDE， ∴平面AEF⊥平面BCDE 又平面AEF∩平面BCDE=EF，AG′⊥EF， ∴AG′⊥平面BCDE，即G′为A在平面BCDE内的射影G， ∴点A在平面BCDE内的射影G在直线EF上。 过G作GH⊥DE，垂足为H，连结AH，则AH⊥DE ∴∠AHG是二面角A-DE-C的平面角，即∠AHG = 设原正方形ABCD的边长为 在折后图的中，. 在折后图的△AEF中，AF=，EF=2AE= ∴△AEF为直角三角形，AG?EF=AE?AF， ∴AG=， 在Rt△ADE中，AH?DE=AD?AE， ∴AH= ∴GH= ∴………………………12分