早教吧作业答案频道 -->数学-->
设四面体A-BCD的六条棱均相等，则二面角A-BC-D的平面角的余弦值为（）A．B．C．0D．
题目详情
设四面体A-BCD的六条棱均相等，则二面角A-BC-D的平面角的余弦值为（ ）
A．
B．
C．0
D．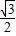
A．
B．
C．0
D．
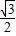
▼优质解答
答案和解析
分析：
设四面体A-BCD的六条棱长都为2，取BC中点O，连接AO，DO，则∠AOD是二面角A-BC-D的平面角．由此利用余弦定理能求出二面角A-BC-D的平面角的余弦值．
设AB=2，∵四面体A-BCD的六条棱均相等，∴AB=BC=AC=BD=CD=AD=2，取BC中点O，连接AO，DO，则AO⊥BC，DO⊥BC，∴∠AOD是二面角A-BC-D的平面角．∵AO=DO==，AD=2，∴cos∠AOD==．故选A．
点评：
本题考查二面角的余弦值的求法，解题时要认真审题，仔细解答，注意余弦定理的合理运用．
分析：
设四面体A-BCD的六条棱长都为2，取BC中点O，连接AO，DO，则∠AOD是二面角A-BC-D的平面角．由此利用余弦定理能求出二面角A-BC-D的平面角的余弦值．
设AB=2，∵四面体A-BCD的六条棱均相等，∴AB=BC=AC=BD=CD=AD=2，取BC中点O，连接AO，DO，则AO⊥BC，DO⊥BC，∴∠AOD是二面角A-BC-D的平面角．∵AO=DO==，AD=2，∴cos∠AOD==．故选A．
点评：
本题考查二面角的余弦值的求法，解题时要认真审题，仔细解答，注意余弦定理的合理运用．
看了 设四面体A-BCD的六条棱均...的网友还看了以下：
四叶玫瑰线的二四象限怎么来的?四叶玫瑰线方程为r=sin(2θ),二四象限范围为（π/2,π）和（ 2020-04-12 …
过定点A(-2,-1),倾斜角为45°的直线与抛物线y=ax平方交于B,C,且bc绝对值是ab绝对 2020-05-13 …
点P在圆C1 X^2+Y^2-8X-4Y+11=0点Q在圆C2 X^2+Y^2+4X+2Y+1=0 2020-05-13 …
在△ABC中，AB=2，AC=4，若点D为边BC的中点，P为△ABC的外心，给出下列数量积：①AB 2020-05-14 …
在矩形ABCD中，已知AB=a，BC=b（a＞b），在AB、AD、CD、CB上分别截取AE、AH、 2020-05-14 …
如图所示，在矩形ABCD中，已知AB=a，BC=b（b＜a），AB，AD，CD，CB上分别截取AE 2020-05-14 …
在△ABC中，BC=10，S△ABC=30，矩形DEFG内接于△ABC，设DE=x，S矩形DEFG 2020-05-14 …
如图,在直角梯形ABCD中,AD平行于BC,角ADC=90度,AD=8,BC=5,CD=4,腰CD 2020-05-16 …
如图,梯形ABCD中,AD∥BC,四边形ABDE为平行四边形,AD延长线交CE与F.（1）求证：F 2020-05-16 …
已知:在平行四边形ABCD中,E为AB的三等分点,F为BC四等分点,连接EF,BD交与G,求BG: 2020-05-16 …