早教吧作业答案频道 -->数学-->
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.
题目详情
在△ABC中,∠BAC=90°,AB=AC,点D和点E均在边BC上,且∠DAE=45°,试猜想BD.DE.EC应满足的数量关系,并写出推理过程.

▼优质解答
答案和解析
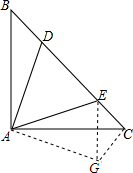 BD2+CE2=DE2,
BD2+CE2=DE2,
理由是:∵AB=AC,
∴把△ABD绕点A逆时针旋转90°至△ACG,可使AB与AC重合,连接EG,
∴AD=AG,BD=CG,∠B=∠ACG,∠BAD=∠CAG,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=°,
∴∠ECG=∠ACB+∠ACG=∠ACB+∠B=45°+45°=90°,
∵∠BAC=90°,∠DAE=45°,
∴∠EAG=∠CAE+∠CAG=∠CAE+∠BAD=90°-45°=45°,
∴∠DAE=∠EAG,
在△DAE和△GAE中,
,
∴△DAE≌△GAE(SAS),
∴DE=EG,
在Rt△ECG中,由勾股定理得:EG2=CE2+CG2,
即BD2+CE2=DE2.
 BD2+CE2=DE2,
BD2+CE2=DE2,理由是:∵AB=AC,
∴把△ABD绕点A逆时针旋转90°至△ACG,可使AB与AC重合,连接EG,
∴AD=AG,BD=CG,∠B=∠ACG,∠BAD=∠CAG,
∵在Rt△BAC中,∠BAC=90°,AB=AC,
∴∠B=°,
∴∠ECG=∠ACB+∠ACG=∠ACB+∠B=45°+45°=90°,
∵∠BAC=90°,∠DAE=45°,
∴∠EAG=∠CAE+∠CAG=∠CAE+∠BAD=90°-45°=45°,
∴∠DAE=∠EAG,
在△DAE和△GAE中,
|
∴△DAE≌△GAE(SAS),
∴DE=EG,
在Rt△ECG中,由勾股定理得:EG2=CE2+CG2,
即BD2+CE2=DE2.
看了 在△ABC中,∠BAC=90...的网友还看了以下:
高一化学,急!20.a,b,c,d,e五种物质,它们是硫及其化合物,已知在一定条件下有如下的转化关 2020-05-13 …
已知a/b=c/d=e/f=2,当b+d≠0时,a+c/b+d=;当b+d+f≠0时,a+c+e/ 2020-05-14 …
已知a,b,c,d,e,f六个数.如果a/b=c/d=e/f(b+d+f≠0),那么a+c+e/b 2020-06-02 …
若a/b=c/d=e/f,则下列各式中正确的是().A.e/f=ac/bdB.e/f=(a+c+e 2020-06-06 …
如图,若AB∥CD,则∠B、∠C、∠E三者之间的关系是()A.∠B+∠C+∠E=180°B.∠B+ 2020-06-12 …
如果a/b=c/d=e/f,那么(a+c+e)/(b+d+f)=a/b成立吗?为什么? 2020-06-12 …
(1)如图①∵∠B+∠D+∠1=180°又∵∠1=∠A+∠2∠2=∠C+∠E∴∠A+∠C+∠E+∠ 2020-06-13 …
已知a/b=c/d=e/f=2/3(b+d+f≠0),求(a+c+e)/(b+d+f)的值. 2020-06-30 …
详细的分比定理的证明whya/b=c/d=e/f=k可推a+c+e/b+d+f=k 2020-07-22 …
急一道数学题已知a/b=c/d=e/f=m/n(b+d+f+...+n≠0)(1)试说明:a+c+e 2020-11-01 …