早教吧作业答案频道 -->数学-->
如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.(1)试猜想线段EF、BE、DF有怎样的数量关系?并证明你的猜想;(2)若点E在BC的延长线上
题目详情
如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.
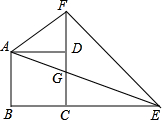
(1)试猜想线段EF、BE、DF有怎样的数量关系?并证明你的猜想;
(2)若点E在BC的延长线上时△EGF与△EFA相似,求BE的长.

(1)试猜想线段EF、BE、DF有怎样的数量关系?并证明你的猜想;
(2)若点E在BC的延长线上时△EGF与△EFA相似,求BE的长.
▼优质解答
答案和解析
(1)猜想:BE=DF+EF,理由如下:
将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,如图1所示,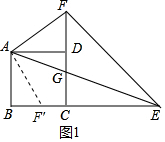
由四边形ABCD为正方形可知点B、C、F′在一条直线上,
∵∠BAF′+∠EAF′+∠GAD=90°,∠BAF′=∠DAF,∠EAF=∠GAD+∠DAF=45°,
∴∠EAF′+∠GAD+∠DAF=90°,∠EAF′=∠EAF=45°.
在△EAF和△EAF′中,
,
∴△EAF≌△EAF′(SAS),
∴EF=EF′,
∴BE=BF′+EF′=DF+EF.
(2)∵△EGF∽△EFA,
∴∠EFG=∠EAF=45°,
∵∠ECF=90°,
∴CE=CF.
设BE=x(x>1),DF=y,则EF=x-y,
在Rt△ECF中,CE=x-1,CF=1+y,EF=x-y,∠ECF=90°,
∴CE2+CF2=EF2,即(x-1)2+(1+y)2=(x-y)2,
∴y=
,
又∵CE=CF,即x-1=1+y,
∴x-1=1+
,化简得:x2-2x-1=0,
解之得:x=1+
或x=1-
(舍去).
∴BE的长为1+
.
将△ADF绕着点A按顺时针方向旋转90°,得△ABF′,如图1所示,

由四边形ABCD为正方形可知点B、C、F′在一条直线上,
∵∠BAF′+∠EAF′+∠GAD=90°,∠BAF′=∠DAF,∠EAF=∠GAD+∠DAF=45°,
∴∠EAF′+∠GAD+∠DAF=90°,∠EAF′=∠EAF=45°.
在△EAF和△EAF′中,
|
∴△EAF≌△EAF′(SAS),
∴EF=EF′,
∴BE=BF′+EF′=DF+EF.
(2)∵△EGF∽△EFA,
∴∠EFG=∠EAF=45°,
∵∠ECF=90°,
∴CE=CF.
设BE=x(x>1),DF=y,则EF=x-y,
在Rt△ECF中,CE=x-1,CF=1+y,EF=x-y,∠ECF=90°,
∴CE2+CF2=EF2,即(x-1)2+(1+y)2=(x-y)2,
∴y=
| x-1 |
| x+1 |
又∵CE=CF,即x-1=1+y,
∴x-1=1+
| x-1 |
| x+1 |
解之得:x=1+
| 2 |
| 2 |
∴BE的长为1+
| 2 |
看了 如图,已知正方形ABCD的边...的网友还看了以下:
已知椭圆y^2/a^2+x^2/b^2=1(a>b>0)的右顶点为A(1,0)过其焦点且垂直长轴的 2020-04-06 …
在路易斯安那我看见一株活着的橡树正在生长1.你能说说橡树的象征意味吗?2.令诗人感到惊奇的是什么? 2020-04-26 …
英语翻译1你们看起来一样2我们都有黑头发3请把这封信交给玛利亚4她的长相如何5她很高像你英语翻译1 2020-05-13 …
对于任意一个矩形A,令另一个矩形B的周长和面积分别是矩形A周长和面积的2倍(1)当矩形A的边长分别 2020-05-13 …
字母a,b各表示一个不超过10的正整数,如果a/b乘以b=8/1,你能知道a,b各表示什么数?字母 2020-05-14 …
古诗词鉴赏:《长沙过贾谊宅》(刘长卿)问题:1.你认为颔联中哪两个字用的得最为传神,找出来古诗词鉴 2020-06-09 …
比较图甲中折线A→D→E→F→…→C与线段AB+BC的长,如果AB=20米,BC=12米.(1)已 2020-06-12 …
A,B兄弟俩比岁数,A对B说,当我是你今年的岁数时,你才5岁.B对A说,当我长到你今sorry,s 2020-06-20 …
假如你热衷集邮,但家长并不支持,于是你向一个学生心声的专栏写信咨询解决的办法。内容包括:1.你的意 2020-06-29 …
写一篇英语短文:1.你和张莉是朋友,同桌,相处友好,你擅长英语,她擅长数学;2.昨天英语测试,她想 2020-07-02 …