早教吧作业答案频道 -->数学-->
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是,位置关系是.请直接写出结论.(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针
题目详情
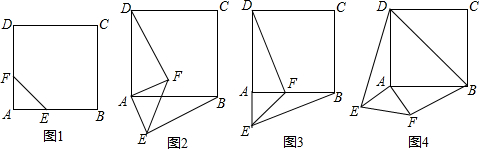
(1)如图1,四边形ABCD是正方形,点E、点F分别在边AB和AD上,且AE=AF.此时,线段BE、DF的数量关系是___,位置关系是___.请直接写出结论.
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
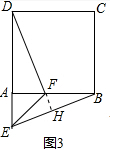
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=___时,直线DF垂直平分BE.请写出计算过程.
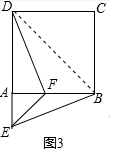
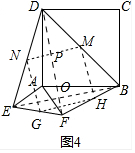
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论:___.
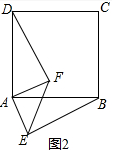
(2)如图2,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当0°<α<90°时,连接BE、DF,此时(1)中的结论是否成立,如果成立,请证明;如果不成立,请说明理由.
(3)如图3,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当α=90°时,连接BE、DF,若正方形的边长为1,猜想当AE=___时,直线DF垂直平分BE.请写出计算过程.
(4)如图4,等腰直角三角形FAE绕直角顶点A顺时针旋转∠α,当90°<α<180°时,连接BD、DE、EF、FB得到四边形BDEF,则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形?请直接写出结论:___.

▼优质解答
答案和解析
(1)如图1中,
∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∵AF=AE,
∴BE=DF,BE⊥DF,
故答案为BE=DF,BE⊥DF
(2)(1)中的结论仍然成立.
理由:如图2中,延长DF交BE于H.
∵四边形ABCD是正方形,
∴AD=AB,AF=AE,∠DAB=∠FAE=90°,
在△DAF和△BAE中,
,
∴△DAF≌△BAE,
∴DF=BE,∠ADF=∠ABR,
∵∠AFD=∠BFH,
∴∠DAF=∠BHF=90°,
∴DF⊥BE.
(3)如图3中,连接BD.
在Rt△ABD中,∵AD=AB=1,
∴BD=
=
,
∵DF垂直平分线段EB,
∴DE=DB=
,
∴AE=DE-AD=
-1,
故答案为
-1.
(4)如图4中,设M、N、G、H分别是BD、DE、EF、BF的中点,连接BE,DF,MN,NG,GH,HM.EB交DF于O,MN交DF于P.
易证:DF=EB,DF⊥EB,
∵DN=NE,DM=MB,
∴MN∥EB,MN=
EB,同理可证GH∥EB,GH=
EB,MH∥DF,MH=
DF,GN∥DF,GN=
DF,
∴MN=NG=GH=HM,
∴四边形MNGH是菱形,
∵MN∥EB,
∴∠DPM=∠DOB=90°,
∵DF∥MH,
∴∠NMH=∠DPM=90°,
∴四边形MNGH是正方形.
故答案为正方形

∵四边形ABCD是正方形,
∴∠DAB=90°,AD=AB,
∵AF=AE,
∴BE=DF,BE⊥DF,
故答案为BE=DF,BE⊥DF
(2)(1)中的结论仍然成立.
理由:如图2中,延长DF交BE于H.

∵四边形ABCD是正方形,
∴AD=AB,AF=AE,∠DAB=∠FAE=90°,
在△DAF和△BAE中,
|
∴△DAF≌△BAE,
∴DF=BE,∠ADF=∠ABR,
∵∠AFD=∠BFH,
∴∠DAF=∠BHF=90°,
∴DF⊥BE.
(3)如图3中,连接BD.

在Rt△ABD中,∵AD=AB=1,
∴BD=
| 12+12 |
| 2 |
∵DF垂直平分线段EB,
∴DE=DB=
| 2 |
∴AE=DE-AD=
| 2 |
故答案为
| 2 |
(4)如图4中,设M、N、G、H分别是BD、DE、EF、BF的中点,连接BE,DF,MN,NG,GH,HM.EB交DF于O,MN交DF于P.

易证:DF=EB,DF⊥EB,
∵DN=NE,DM=MB,
∴MN∥EB,MN=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=NG=GH=HM,
∴四边形MNGH是菱形,
∵MN∥EB,
∴∠DPM=∠DOB=90°,
∵DF∥MH,
∴∠NMH=∠DPM=90°,
∴四边形MNGH是正方形.
故答案为正方形
看了 (1)如图1,四边形ABCD...的网友还看了以下:
已知b分之a=d分之c=f分之e=2且b+d+f≠0.(1)b+d+f分之a+c+e=(2)b-d 2020-06-09 …
已知b分之a=d分之c=f分之e,求b+d+f分之a+c+e的值 2020-06-09 …
已知b分之a=d分之C=ff分之e=3分之2,求b+d+f分之A+C+E求过程 2020-06-09 …
A、B、C、D、E、F、G、H、I、J分别代表十种不同的有机物(其中A是化学工业重要原料之一).它 2020-06-12 …
A、B、C、D、E、F、G、H、I、J分别代表十种不同的有机物(其中A是化学工业重要原料之一).它 2020-06-12 …
D具有酸性,F具有中性,在D和F中加酸和高锰酸钾共热时,都被氧化放出CO2,求D和F的结构式,D和 2020-06-12 …
有两个关于变上限积分可导,连续的问题搞不懂?有如下两个结论如果函数f(x)在[a,b]上可导有两个 2020-06-18 …
关于拉格朗日中值定理两个前提条件:f(x)在[a,b]上连续,在(a,b)上可导.若[a,b]换成 2020-06-22 …
F是一种冶疗艾滋病的新药(结构简式见右图),已知F分子中苯环与-NH-CO-O-基团在同一平面内, 2020-07-10 …
7=b分之a=d分之c=f分之e,求b+d+f分之a+c+e的值、、快快吖、、、 2020-07-14 …