早教吧作业答案频道 -->数学-->
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方(1)求圆C的方程;(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N
题目详情
已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的右上方
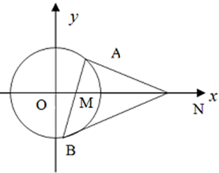
(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.

(1)求圆C的方程;
(2)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在定点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.
▼优质解答
答案和解析
(1)设圆心C(a,0)(a>-
),
∵直线l:4x+3y+10=0,半径为2的圆C与l相切,
∴d=r,即
=2,
解得:a=0或a=-5(舍去),
则圆C方程为x2+y2=4;
(2)当直线AB⊥x轴,则x轴平分∠ANB,
若x轴平分∠ANB,则kAN=-kBN,即
+
=0,
整理得:2x1x2-(t+1)(x1+x2)+2t=0,即
-
+2t=0,
解得:t=4,
当点N(4,0),能使得∠ANM=∠BNM总成立.
| 5 |
| 2 |
∵直线l:4x+3y+10=0,半径为2的圆C与l相切,
∴d=r,即
| |4a+10| |
| 5 |
解得:a=0或a=-5(舍去),
则圆C方程为x2+y2=4;
(2)当直线AB⊥x轴,则x轴平分∠ANB,
若x轴平分∠ANB,则kAN=-kBN,即
| k(x1-1) |
| x1-t |
| k(x2-1) |
| x2-t |
整理得:2x1x2-(t+1)(x1+x2)+2t=0,即
| 2(k2-4) |
| k2+1 |
| 2k2(t+1) |
| k2+1 |
解得:t=4,
当点N(4,0),能使得∠ANM=∠BNM总成立.
看了 已知直线l:4x+3y+10...的网友还看了以下:
常温下向100mL0.1mol?L-1HA溶液中逐滴加入0.2mol?L-1KOH溶液,图中所示曲 2020-05-14 …
已知质点的运动方程为x=2t,y=2t平方,式中x,y的单位为s,求t=2s时,质点速度和t=2s 2020-05-14 …
椭圆方程问题已知椭圆方程x^2/a^2+Y^2/b^2=1,又已知椭圆外一点P(x0,y0),过P 2020-05-15 …
求下列各二次函数图象的顶点坐标1.已知抛物线Y=X的平方-4X加32.已知二次函数Y=7X的平方加 2020-06-14 …
已知二次涵数Y=X的二次方-(2m+4)X+(m-2)(m+2)的图象与Y轴交点C在原点下方,与X 2020-06-29 …
已知光滑曲线C:x=x(t),y=y(t),z=z(t)在点(x(t0),y(t0),z(t0)) 2020-07-10 …
经过点(-1,1)且垂直於直线3x-2y=0的直线方程是?己知圆C:x^2+y^2-2x+4y=0 2020-07-30 …
切线方程切点坐标已知:曲线方程为Y=X的3次方-3X求切线方程X轴的切点坐标已知:曲线方程Y=E的 2020-07-31 …
一沿X轴正方向的力作用在一质量为3KG的质点上,已知质点的运动方程为X=3T-4T*一沿X轴正方向 2020-07-31 …
1.若点A(a-2,3),与B(4,-3)关于原点对称,则a=2.已知x=-1是方程x-a1.若点A 2021-02-14 …