早教吧作业答案频道 -->物理-->
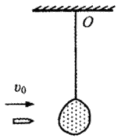
如图所示,一砂袋用不可伸长的轻绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度大小为v0,打入砂袋后二者共同摆动的最大摆角为θ
题目详情
如图所示,一砂袋用不可伸长的轻绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度大小为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为7m,弹丸和砂袋形状大小均忽略不计,子弹击中沙袋后漏出的沙子质量忽略不计,重力加速度为g,求:
①轻绳长度L(用θ、g、v0表示);
②两粒弹丸的水平速度之比v0/v为多少?
①轻绳长度L(用θ、g、v0表示);
②两粒弹丸的水平速度之比v0/v为多少?

▼优质解答
答案和解析
①设碰后弹丸和砂袋的共同速度为v1,细绳长为L,
弹丸击中砂袋过程系统动量守恒,以向右为正方向,
由动量守恒定律得::mv0=(m+7m)v1,
砂袋摆动过程中只有重力做功,机械能守恒,
由机械能守恒定律得:
•8m
=8mgL(1-cosθ),
解得:L=
;
②设第二粒弹丸击中砂袋后弹丸和砂袋的共同速度为v2,
以向右为正方向,由动量守恒定律得:mv-(m+7m)v1=(m+8m)v2
由机械能守恒定律得:
•9m
=9mgL(1-cosθ),
解得:v2=v1,联解上述方程得
=
答:①轻绳长度L为
;
②两粒弹丸的水平速度之比
为8:17.
弹丸击中砂袋过程系统动量守恒,以向右为正方向,
由动量守恒定律得::mv0=(m+7m)v1,
砂袋摆动过程中只有重力做功,机械能守恒,
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 1 |
解得:L=
| ||
| 128g(1-cosθ) |
②设第二粒弹丸击中砂袋后弹丸和砂袋的共同速度为v2,
以向右为正方向,由动量守恒定律得:mv-(m+7m)v1=(m+8m)v2
由机械能守恒定律得:
| 1 |
| 2 |
| v | 2 2 |
解得:v2=v1,联解上述方程得
| v0 |
| v |
| 8 |
| 17 |
答:①轻绳长度L为
| ||
| 128g(1-cosθ) |
②两粒弹丸的水平速度之比
| v0 |
| v |
看了 如图所示,一砂袋用不可伸长的...的网友还看了以下:
以下有关工作最迟开始时间的说法中,正确的有( )。 A.工作最迟开始时间等于其紧后工作最迟开始 2020-05-19 …
袋子里共有415只小球,第一次从袋子里取出1只小球,第二次从袋子里取出3只小球,第三次从袋子里取出 2020-06-16 …
数据结构:一个事件的最迟开始时间为以该事件为尾的弧的活动最迟开始时间与该活动的持续时间的差.这句. 2020-06-22 …
双代号网络图求解,要步骤,搞不懂在某工程双代号网络计划中,工作N的最早开始时间和最迟开始时间分别为 2020-06-22 …
二级建造师网络计划中,工作A的紧后工作是B和C,工作B最迟开始时间是14,最早开始时间是10,工作 2020-06-22 …
一袋米,第一次取出全部的一半多1.5kg,第二次取出余下的一半少2kg,最后袋中还剩20kg,这袋 2020-06-26 …
有一袋大米,第一次取出全部的一半多1.5kg,第二次取出余下大米的一半少2kg,最后袋中的大米还剩 2020-07-14 …
材料一:固体废弃物是指人类在生产、消费、生活和其他活动中产生的固态、半固态废弃物质。目前固体废弃物中 2020-11-05 …
怎么计算最早时间,最早结束,最迟开始,最迟结束工序结点编号完成时间A1-23B1-34C2-45D3 2020-12-01 …
上世纪80年代,广东零售业最先开始向顾客附赠塑料购物袋,此后迅速普及大江南北。当年的媒体曾热情讴歌这 2020-12-26 …