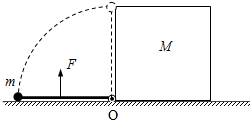
如图所示，长为L的轻杆一端连着质量为m的小球，另一端用活动铰链固接于水平地面上的O点，初始时小球静止于地面上，边长为L、质量为M的正方体左侧静止于O点处．现在杆中点处施加一大

Question

如图所示，长为L的轻杆一端连着质量为m的小球，另一端用活动铰链固接于水平地面上的O点，初始时小球静止于地面上，边长为L、质量为M的正方体左侧静止于O点处．现在杆中点处施加一大小始终为(6mg)/(π)（g为重力加速度）、方向始终垂直杆的拉力，经过一段时间后撤去F，小球恰好能到达最高点．忽略一切摩擦，试求：

（1）拉力所做的功；
（2）拉力撤去时小球的速度大小；
（3）若小球运动到最高点后由静止开始向右倾斜，求杆与水平面夹角为θ时（正方体和小球还未脱落），正方体的速度大小．

Answer 1

（1）根据动能定理可得：W_F-mgL=0                              
力F所做的功为W_F=mgL                                
（2）设撤去F时，杆与水平面夹角为α，撤去F前，有：
W_F=(6mg)/(π)×(L)/(2)α=mgL，
解得：α=(π)/(3)
根据动能定理有：mgL-mgLsinα=(1)/(2)mv²                        
得撤去F时小球的速度为：v=√(gL(2-√(3)))
（3）设杆与水平面夹角为θ时，杆的速度为v₁，正方体的速度为v₂
v₂=v₁sinθ                                              
系统机械能守恒有：
mg（L-Lsinθ）=(1)/(2)mv₁²+(1)/(2)Mv₂²                 
解得：v₂=√((2mgL(1-sinθ)sin2θ)/(m+Msin2θ))．
答：（1）力F所做的功为mgL；
（2）力F撤去时小球的速度为√(gL(2-√(3)))；
（3）正方体的速度大小为√((2mgL(1-sinθ)sin2θ)/(m+Msin2θ))．