早教吧作业答案频道 -->数学-->
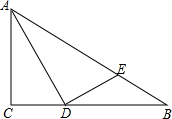
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且BEAB=14.(1)求线段BD的长;(2)求∠ADC的正切值.
题目详情
已知,如图,在Rt△ABC中,∠ACB=90°,AB=4,AD是∠BAC的平分线,过点D作DE⊥AD,垂足为点D,交AB于点E,且
=
.
(1)求线段BD的长;
(2)求∠ADC的正切值.
| BE |
| AB |
| 1 |
| 4 |

(1)求线段BD的长;
(2)求∠ADC的正切值.
▼优质解答
答案和解析
(1)∵DE⊥AD,
∴∠BDE=∠CAD=90°-∠CDA,
∵∠CAD=∠DAB,
∴∠BAD=∠BDE,
∵∠B=∠B,
∴△BED∽△BDA,
∴BD2=BE•BA,
∵AB=4,
=
,
∴BE=1,
∴BD2=1×4=4,
∴BD=2;
(2),∵DE⊥AD,
∴∠AED=90°-∠DAE,
∵∠ADE=90°-∠CAD,
∵∠CAD=∠DAB,
∴∠ADE=∠AED,
∵△BED∽△BDA,
∴
=
,
∴tan∠ADC=tan∠AED=
=
=
=2.
∴∠BDE=∠CAD=90°-∠CDA,
∵∠CAD=∠DAB,
∴∠BAD=∠BDE,
∵∠B=∠B,
∴△BED∽△BDA,
∴BD2=BE•BA,
∵AB=4,
| BE |
| AB |
| 1 |
| 4 |
∴BE=1,
∴BD2=1×4=4,
∴BD=2;
(2),∵DE⊥AD,
∴∠AED=90°-∠DAE,
∵∠ADE=90°-∠CAD,
∵∠CAD=∠DAB,
∴∠ADE=∠AED,
∵△BED∽△BDA,
∴
| AD |
| AE |
| AB |
| BD |
∴tan∠ADC=tan∠AED=
| AD |
| AE |
| AB |
| BD |
| 4 |
| 2 |
看了 已知,如图,在Rt△ABC中...的网友还看了以下:
24 (a+b)/(c+d)=(√a^2+b^2)/√ (c^2+d^2)成立证明:(1)a/b= 2020-05-14 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
A.πA,D(σC=D(R×S))B.πA,R,D(σS,C=R,D/(R×S))C.πA,R,D( 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σR.C=S.D(R×S))C.πA,R.D(σ 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σS.C=R.D(R×S))C.πA,R.D(σ 2020-05-26 …
如果正数a,b,c,d满足a+b=cd=4,那么()A.ab≤c+d且等号成立时a,b,c,d的取 2020-07-09 …
用Matlab求解方程组?如何用数值法啊?,a,b,c,d是未知量s1=(a/((4*pi*b*c 2020-07-23 …
A,B,C,D四个数的和为59,问A^2+B^2+C^2+D^2,A^3+B^3+C^3+D^3, 2020-07-28 …
多元一次方程求解a=0.1072(a+b+c+d+e)b=0.041(a+b+c+d+e)c=0.2 2020-12-14 …
请问谁知道用matlab求解多元超越方程组的方法或思路或函数不?形如:a*(1+a+a^3+d+d^ 2020-12-14 …