早教吧作业答案频道 -->数学-->
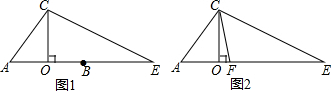
CO是△ACE的高,点B在OE上,OB=OA,AC=BE(1)如图1,求证:∠A=2∠E;(2)如图2,CF是△ACE的角平分线.①求证:AC+AF=CE;②判断三条线段CE、EF、OF之间的数量关系,并给出证明.
题目详情
CO是△ACE的高,点B在OE上,OB=OA,AC=BE
(1)如图1,求证:∠A=2∠E;
(2)如图2,CF是△ACE的角平分线.
①求证:AC+AF=CE;
②判断三条线段CE、EF、OF之间的数量关系,并给出证明.
(1)如图1,求证:∠A=2∠E;
(2)如图2,CF是△ACE的角平分线.
①求证:AC+AF=CE;
②判断三条线段CE、EF、OF之间的数量关系,并给出证明.

▼优质解答
答案和解析
证明:(1)连接CB,由AO=OB,CO⊥AB,
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
,
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
∴CA=CB,
∴∠A=∠CBA,
∵AC=BE,
∴BE=CB,
∴∠E=∠BCE,
∴∠A=∠CBA=∠BCE+∠E=2∠E;
(2)①在CE上截取CH=CA,连接FH,
∵∠ACF=∠ECF,CF=CF,
在△FCA与△FCH中,
|
∴△FCA≌△FCH,
∴AF=HF,∠A=∠CHF=∠HFE+∠E=2∠E,
∴∠HFE=∠E,
∴AF=HE,
即CE=CH+HE=CA+AF;
②在①的基础上,BE=AC,AO=OB,
∴CE=CA+AF
=BE+AO+OF
=EF-FB+OB+OF
=EF+OF+OF
=EF+2OF.
看了 CO是△ACE的高,点B在O...的网友还看了以下:
已知向量a=(2,1),向量b=(-8,6)(1)已知向量a=(-1,2),向量b=(1,-2)求 2020-04-05 …
半径是R的圆的周长C=2πR,下列说法正确的是()A、C,π,R是变量,2是常量B、C是变量,2, 2020-04-12 …
在圆的周长公式C=2πr中,下列说法错误的是()A.C,π,r是变量,2是常量B.C,r是变量,2 2020-04-12 …
在圆的周长公式C=2πR中.常量与变量分别是().(A)2是常量,C、π、R是变量(B)2兀是常量 2020-04-12 …
圆的周长公式C=2πR中,下列说法错误的是()A.C、π、R是变量,2是常量B.C、R是变量,2π 2020-04-12 …
圆周长公式C=2πR中,下列说法正确的是()A.π、R是变量,2为常量B.C、R为变量,2、π为常 2020-05-13 …
已知向量a=(根号3,1)且向量b与a的夹角为30度,求b向量a,b满足:/a向量-b向量/=5a 2020-05-14 …
圆的周长公式C=2πR中,下列说法正确的是()A.π、R是自变量,2是常量B.C是因变量,R是自变 2020-07-25 …
向量(1220:5:24)已知向量a,b,c满足:向量a+向量b+向量c=0向量,且|a|=1,| 2020-08-01 …
高一向量两道小题,在线求解1、已知向量a,b,c满足a+b+c=0,模分别为a=1,b=√2,c= 2020-08-02 …