如图，在△ABC中，∠C=90°，∠BAC=60°，AC=1，点D在BC上，点E在AB上，使得△ADE是等腰直角三角形，∠ADE=90°，求BE的长．（提示：可以运用“直角三角形中，30°角所对的直角边等于斜边

Question

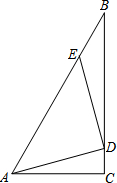如图，在△ABC中，∠C=90°，∠BAC=60°，AC=1，点D在BC上，点E在AB上，使得△ADE是等腰直角三角形，∠ADE=90°，求BE的长．（提示：可以运用“直角三角形中，30°角所对的直角边等于斜边的一半”）．

Answer 1

考点：
全等三角形的判定与性质 含30度角的直角三角形 勾股定理 平行线分线段成比例
专题：

分析：
过点EF作∥AC，交BC于点F，证明△ADC和△DEF全等，得出DF=AC=1，设CD=x，利用平行线分线段成比例定理，列出比例式，列方程解答．

过点E作EF作∥AC，交BC于点F，∴∠BFC=∠C=90°，∵∠C=90°，∠BAC=60°，∴∠B=30°∴AB=2AC=2，在Rt△ABC中，由勾股定理得：CB=AB2-AC2=22-12=3，∵△ADE是等腰直角三角形，∴DE=DA，∵∠DAC+∠ADC=90°，∠EDF+∠ADC=90°，∴∠DAC=∠EDF在△ADC和△DEF中∠DAC=∠EDF∠C=∠EFD=90°DA=DE∴△ADC≌△DEF（AAS），∴DF=AC=1，设CD=x，所以EF=x，BF=3-1-x∵EF∥AC∴EFAC=BFBC即x1=3-1-x3解得：x=2-3．即BE=2-3．
点评：
本题考查了全等三角形的性质和判定、勾股定理、平行线分线段成比例定理，解题的关键是添加辅助线构造全等三角形，另外利用平行线成比例定理，列方程求线段的长度，也是经常用到的方法．