早教吧作业答案频道 -->数学-->
如图,点D、E分别在△ABC的边AB、AC上,AD=4,BD=5,DE∥BC,∠ACD=∠B.(1)求边AC的长;(2)若S△ADE=2,求S△BCD的面积.
题目详情
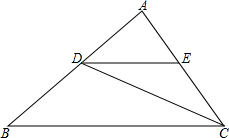 如图,点D、E分别在△ABC的边AB、AC上,AD=4,BD=5,DE∥BC,∠ACD=∠B.
如图,点D、E分别在△ABC的边AB、AC上,AD=4,BD=5,DE∥BC,∠ACD=∠B.(1)求边AC的长;
(2)若S △ADE =2,求S △BCD 的面积.
▼优质解答
答案和解析
考点:
相似三角形的判定与性质
专题:
分析:
(1)因为DE∥BC,所以△ADE∽△ABC,利用相似三角形的性质:对应边的比值相等即可求出AC的长;(2)由(1)可知△ADE∽△ABC,所以可得到△ABC的面积,利用高相等的三角形面积之比等于底之比可求出△DEC的面积,进而可求出S△BCD.
(1)∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=AE:AC,∵AD=4,BD=5,∴AE:AC=4:9,∵DE∥BC,∴∠B=∠ADE,∵∠ACD=∠B.∴∠ADE=∠ACD,∵∠A=∠A,∴△ADE∽△ACD,∴AD:AC=AE:AD,∴AD2=AC?AE,即16=49AC2,∴AC=6,(2)∵△ADE∽△ABC,S△ADE=2,∴S△ABC=818,∵AE:CE=4:5,S△ADE=2,∴S△DEC=52,∴S△BCD=818-52=618.
点评:
本题考查了相似三角形的判定和性质以及平行线的性质,熟悉相似三角形的性质:相似三角形的面积比是相似比的平方是解题关键,题目的综合性较强,难度不小.
考点:
相似三角形的判定与性质
专题:
分析:
(1)因为DE∥BC,所以△ADE∽△ABC,利用相似三角形的性质:对应边的比值相等即可求出AC的长;(2)由(1)可知△ADE∽△ABC,所以可得到△ABC的面积,利用高相等的三角形面积之比等于底之比可求出△DEC的面积,进而可求出S△BCD.
(1)∵DE∥BC,∴△ADE∽△ABC,∴AD:AB=AE:AC,∵AD=4,BD=5,∴AE:AC=4:9,∵DE∥BC,∴∠B=∠ADE,∵∠ACD=∠B.∴∠ADE=∠ACD,∵∠A=∠A,∴△ADE∽△ACD,∴AD:AC=AE:AD,∴AD2=AC?AE,即16=49AC2,∴AC=6,(2)∵△ADE∽△ABC,S△ADE=2,∴S△ABC=818,∵AE:CE=4:5,S△ADE=2,∴S△DEC=52,∴S△BCD=818-52=618.
点评:
本题考查了相似三角形的判定和性质以及平行线的性质,熟悉相似三角形的性质:相似三角形的面积比是相似比的平方是解题关键,题目的综合性较强,难度不小.
看了 如图,点D、E分别在△ABC...的网友还看了以下:
已知椭圆的方程x²/a²+y²/b²=1(a>b>0),点p(-3,1)在直线x=-a²/c上,过点 2020-03-30 …
有两栋相同的楼房,两人在六楼A,C上看两楼之间的空地上的一盆花E是,视线与水平方向的夹角(俯角)相 2020-05-17 …
在计算可支配月收入过程中,不应扣除的项目是()。A.所得税B.缴存的住房公积金C.上缴的失业保险费D 2020-05-22 …
系膜增生性肾小球肾炎电镜下可见A:上皮细胞足突消失B:上皮下驼峰样沉积物C:上皮下沉积物伴基 2020-06-07 …
证明f(x)在[a,b]与[b,c]一致连续,则f(x)在[a,c]上一致连续 2020-06-12 …
如何证明积分中值定理的推论?重谢!设函数f和g在[a,b]上可积.若g为单调函数且在(a,b)上不 2020-07-30 …
如果积分的上界是a下界是b那么a,b是开区间(a,b)还是[a,b]?如果a>c>b,上下界分别a 2020-07-31 …
求证明…不胜感激…第二积分中值定理第二积分中值定理第二积分中值定理:若1)f(x)在[a,b]上非 2020-08-01 …
(本小题满分14分)已知椭圆的左焦点为F,左右顶点分别为A,C上顶点为B,过F,B,C三点作,其中 2020-08-01 …
原函数积分加反函数积分…我总不可能画个图吧…怎办…原函数f(x)在[a,b]上单调递增,a>0,f( 2020-11-08 …