早教吧作业答案频道 -->数学-->
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.(1)求证:∠ADC=∠DCE+∠EAF;(2)求证:AF•AD=AB•EF.
题目详情
已知:如图,在△ABC中,点D、E分别在边BC、AB上,BD=AD=AC,AD与CE相交于点F,AE2=EF•EC.
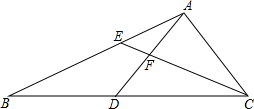
(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.

(1)求证:∠ADC=∠DCE+∠EAF;
(2)求证:AF•AD=AB•EF.
▼优质解答
答案和解析
证明:(1)∵BD=AD=AC,
∴∠B=∠BAD,∠ADC=∠ACD,
∵AE2=EF•EC,
∴
=
,
∵∠E=∠E,
∴△EAF∽△ECA,
∴∠EAF=∠ECA,
∴∠ADC=∠ACD=∠ACE+∠ECB=∠DCE+∠EAF;
(2)∵△EAF∽△ECA,
∴
=
,即
=
,
∵∠EFA=∠BAC,∠EAF=∠B,
∴△FAE∽△ABC,
∴
=
,
∴FA•AC=EF•AB,
∵AC=AD,
∴AF•AD=AB•EF.
∴∠B=∠BAD,∠ADC=∠ACD,
∵AE2=EF•EC,
∴
| AE |
| CE |
| EF |
| AE |
∵∠E=∠E,
∴△EAF∽△ECA,
∴∠EAF=∠ECA,
∴∠ADC=∠ACD=∠ACE+∠ECB=∠DCE+∠EAF;
(2)∵△EAF∽△ECA,
∴
| AE |
| EF |
| AC |
| AF |
| AF |
| EF |
| AC |
| AE |
∵∠EFA=∠BAC,∠EAF=∠B,
∴△FAE∽△ABC,
∴
| FA |
| AB |
| EF |
| AC |
∴FA•AC=EF•AB,
∵AC=AD,
∴AF•AD=AB•EF.
看了 已知:如图,在△ABC中,点...的网友还看了以下:
noip的初赛问题..和或..设A=True,B=False,C=True,D=False,以下逻辑 2020-03-31 …
有A、B、C、D四根导线,其中A、B、C是铝线,D是镍铬合金线.A、B粗细相同,A比B短;B、C长 2020-04-13 …
图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D线 2020-04-23 …
15.图中构成东西半球分界线的两条经线是()A.A线和C线B.A线和D线C.B线和C线D.B线和D 2020-04-23 …
读图完成问题小题1:位于东西半球分界线上的点是A.F点B.D点C.C点D.G点小题2:同时位于东半 2020-04-23 …
选出下列各项中注音有误的一项:()A.淙淙cóng不啻chì谄媚chǎnB.郴州chēn悼念dào 2020-05-16 …
I'm good at basketball.A.play B.plays C.playing D 2020-05-17 …
数字推理的问题5219,1,4,3,40,()A、81、B、80、C、120、D、12152213 2020-06-06 …
如果abcd>0,a>c,bcd<0,则有()A.a>0,b<0,c>0,d>0B.a<0,b<0 2020-07-09 …
选出下列词语中注音有误的一项:()A.辘lù轳山麓lù滴dī水嘀dí咕B.嫡dí系锋镝dí墒shā 2020-07-22 …