如图甲所示，用一轻质绳拴着一质量为m的小球，在竖直平面内做圆周运动（不计一切阻力），小球运动到最高点时绳对小球的拉力为F，小球在最高点的速度大小为v，其F-v2图象如图乙所示，

Question

如图甲所示，用一轻质绳拴着一质量为m的小球，在竖直平面内做圆周运动（不计一切阻力），小球运动到最高点时绳对小球的拉力为F，小球在最高点的速度大小为v，其F-v²图象如图乙所示，则
（　　）

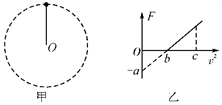
A. 轻质绳长为

(b)/(a)

B. 当地的重力加速度为

(a)/(m)

C. 当v²=c时，轻质绳的拉力大小为

(ac)/(b)+a

D. 只要v²≥b，小球在最低点和最高点时绳的拉力差均为6a

Answer 1

A、在最高点，根据牛顿第二定律得，F+mg=m(v2)/(L)，解得F=m(v2)/(L)-mg，
根据纵轴截距知，a=mg，则重力加速度g=(a)/(m)，图线的斜率k=(m)/(L)=(a)/(b)，解得轻质绳长L=(mb)/(a)，故A错误，B正确．
C、当v²=c时，绳子的拉力F=m(v2)/(L)-mg=(mc)/(L)-mg=(ac)/(b)-a，故C错误．
D、在最高点，F=m(v2)/(L)-mg，设最低点的速度为v′，根据动能定理得，mg•2L=(1)/(2)mv′2-(1)/(2)mv2，根据牛顿第二定律得，F′-mg=m(v′2)/(L)，解得F′=mg+m(v′2)/(L)，
拉力差△F=F′-F=2mg+(mv′2-mv2)/(L)=6mg=6a，故D正确．
故选：BD．