早教吧作业答案频道 -->数学-->
设f(x)=,利用课本中推导等差数列前n项和公式的方法,可求得f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)的值是()A.B.4C.D.12
题目详情
设f(x)=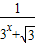 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)的值是( )
,利用课本中推导等差数列前n项和公式的方法,可求得f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)的值是( )
A.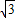
B.4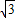
C.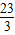
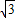
D.12
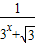 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)的值是( )
,利用课本中推导等差数列前n项和公式的方法,可求得f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)的值是( )A.
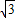
B.4
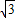
C.
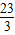
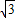
D.12
▼优质解答
答案和解析
【答案】分析:先求出f(x)+f(1-x)的值为常数,然后利用倒序相加法求出代数式的和,从而求出所求.∵f(x)=,∴f(x)+f(1-x)=+=+=,设S=f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)所以S=f(12)+f(11)+…+f(0)+…+f(-10)+f(-11)两个式子相加得2S=×24=8∴S=4故选B.点评:本题主要考查倒序相加求和法,注意代数式的化简方法,基本知识的灵活应用,考查计算能力,属于基础题.
看了 设f(x)=,利用课本中推导...的网友还看了以下:
下列关于美国南北战争说法正确的是()A.时间发生在19世纪70年代B.南北矛盾的焦点是奴隶制的存废 2020-05-12 …
维新变法运动期间,资产阶级维新派大量办报的主要原因是()A.清政府的重视与推动B.国人休闲方式变化 2020-05-13 …
下列关于力的说法中错误的是A.相互接触的物体才会发生力的作用B.小孩用力推墙,他同时也受到墙的推力 2020-05-13 …
某校准备邀请一位学者作报告,下列适合出现在下图海报内容中的是A.中国的分封制度B.拜占廷帝国的衰亡 2020-05-16 …
工业革命期间资本主义国家推行的社会立法首先开始于[]A.《矿井法》B.《公共卫生法》C.《工会法》 2020-05-17 …
外国旅游者在中国境内犯法,要受到( )的制裁。 A.国际法B.中国法律C.所属国的法律D.国 2020-05-19 …
在我国,可以成为期货交易所会员的是( )。 A.自然人B.法人C.境内登记注册的法人D.境内注册 2020-06-04 …
不属于当代中国守法的范围的是()。A.地方性法规B.法院的裁定书C.特别行政区的法律D.习惯 2020-06-04 …
如何由文法推导语法树?(编译原理)给定一个文法规则来推导语法树结果唯一吗? 2020-06-05 …
甲乙分别用40N,50N,推同一个木箱,木箱重20kg,已知甲乙分别都把物体推了20m,则一下说法 2020-06-06 …