早教吧作业答案频道 -->数学-->
如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.(1)求证:AS•BC=AB•SR.(2)求正方形PQRS的边长.
题目详情
如图,AD是△ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=30cm,AD=20cm,四边形PQRS是正方形.
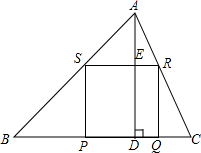
(1)求证:AS•BC=AB•SR.
(2)求正方形PQRS的边长.

(1)求证:AS•BC=AB•SR.
(2)求正方形PQRS的边长.
▼优质解答
答案和解析
(1)证明:∵四边形PQRS是正方形,
∴SR∥BC,
∴△ASR∽△ABC,
∴AS:AB=SR:BC,
∴AS•BC=AB•SR.
(2) 设正方形PQRS的边长为xcm,
∵AD是△ABC的高,SR∥BC,
∴AE是△ASR的高,
则AE=AD-ED=20-x(cm),
∵△ASR∽△ABC,
∴
=
,
∴
=
,
解得:x=12,
∴正方形PQRS的边长为12cm.
∴SR∥BC,
∴△ASR∽△ABC,
∴AS:AB=SR:BC,
∴AS•BC=AB•SR.
(2) 设正方形PQRS的边长为xcm,
∵AD是△ABC的高,SR∥BC,
∴AE是△ASR的高,
则AE=AD-ED=20-x(cm),
∵△ASR∽△ABC,
∴
| SR |
| BC |
| AE |
| AD |
∴
| x |
| 30 |
| 20-x |
| 20 |
解得:x=12,
∴正方形PQRS的边长为12cm.
看了 如图,AD是△ABC的高,点...的网友还看了以下:
1.已有定义inta[10],*p;则正确的赋值语句是().A.p=100;B.p=a[5];C.p 2020-03-31 …
在循环双链表的p所指节点之后插入s所直接点操作A,p->next=s;s->prior=p;p->n 2020-03-31 …
设a=(√5-1)/2,求(a^5+a^4-2a^3-a^2-a+2)/a^3-a∵2a=√5-1 2020-04-05 …
计算题(P/A,10%,4)=3.1699(P/F,10%,1)=0.9091(P/A,10%,5 2020-04-07 …
已知文法G2=(VT={a,',',(,)},VN{S,L},S,P),其中P为, S→(L)|a 2020-05-26 …
一、已知数集M满足条件:若a∈M,则(1+a)/(1-a)∈M(a≠0,a≠±1)(1)若3∈M, 2020-07-30 …
P(A)=0不能推出A=空?P(B)=1不能推出B为S?一本辅导书上说P(A)=0不能推出A=空P( 2020-11-03 …
有变量定义如下,inta[2][3],*p,(*q)[3];以下赋值语句错误的是A.p=a;有变量定 2020-12-31 …
递回关系式的运算公式(数列)以下是推导一个公式"a=a+r(1-p^n)/(1-p)"的过程a=p* 2021-01-13 …
函数f[x]=logaXa大于0,且a不等于1,在2,3上最大值为1,则a=当a大于1时,f(x)图 2021-01-15 …