早教吧作业答案频道 -->数学-->
如图,AD=CB,E、F是AC上两动点,且有DE=BF.(1)若点E、F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;(2)若点E、F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还
题目详情
如图,AD=CB,E、F是AC上两动点,且有DE=BF.
(1)若点E、F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E、F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E、F不重合,则AD和CB平行吗?请说明理由.
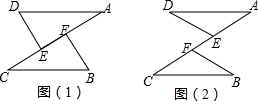
(1)若点E、F运动至如图(1)所示的位置,且有AF=CE,求证:△ADE≌△CBF;
(2)若点E、F运动至如图(2)所示的位置,仍有AF=CE,则△ADE≌△CBF还成立吗?为什么?
(3)若点E、F不重合,则AD和CB平行吗?请说明理由.

▼优质解答
答案和解析
(1)证明:∵AF=CE,
∴AF+EF=CE+EF,即AE=CF,
在△ADE和△CBF中,
∵
,
∴△ADE≌△CBF(SSS);
(2)△ADE≌△CBF成立,
∵AF=CE,
∴AF-EF=CE-EF,即AE=CF,
在△ADE和△CBF中,
∵
,
∴△ADE≌△CBF(SSS);
(3)AD∥CB,
∵△ADE≌△CBF,
∴∠A=∠C,
∴AD∥CB.
∴AF+EF=CE+EF,即AE=CF,
在△ADE和△CBF中,
∵
|
∴△ADE≌△CBF(SSS);
(2)△ADE≌△CBF成立,
∵AF=CE,
∴AF-EF=CE-EF,即AE=CF,
在△ADE和△CBF中,
∵
|
∴△ADE≌△CBF(SSS);
(3)AD∥CB,
∵△ADE≌△CBF,
∴∠A=∠C,
∴AD∥CB.
看了 如图,AD=CB,E、F是A...的网友还看了以下:
如图,一质点p在数轴上从 距原点1个单位的a点处向原点方向跳动,第一次跳到oa的中点A1处,第二次 2020-05-13 …
某点p从距原点1个单位的a点处向原点方向跳动,第一次跳动到oa的中点a1处 第二次从a1点跳动到o 2020-05-13 …
1.a和b属于正整数,a的100次方是一个120位数,a的b次方是一个10位数,求b值?2.f(x 2020-05-17 …
根据《建筑法》规定,发包单位将工程发包给不具有相应资质条件的承包单位的,( )A.警告 B. 2020-05-18 …
一道政治计算题.请教各位2011年a国与b国的货币汇率为1:6,b国生产甲商品的某企业,生产每件商 2020-05-20 …
在Windows操作系统的发展过程中,从哪一个操作系统开始,以后的操作系统都是32位的?A.Wind 2020-05-24 …
试题二(共15)阅读以下关于 AD574(12 位的 A/D 转换器)的叙述,回答问题 1 至问题 2020-05-26 …
扬压力测量时,两次读数差不得大于压力表最小刻度单位的( ) A,1/2A.1/3B.1/5 2020-05-27 …
请用函数解:在一条公路的一侧有某单位的A,B两个加工点,A到公路的距离AC为1km,B到公路的请用 2020-06-02 …
用函数解:在一条公路的一侧有某单位的A,B两个加工点,A到公路的距离AC为1km,B到公路的距用函 2020-06-02 …