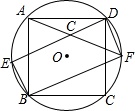
正方形ABCD内接于O，如图所示，在劣弧AB上取一点E，连接DE、BE，过点D作DF∥BE交O于点F，连接BF、AF，且AF与DE相交于点G，求证：（1）四边形EBFD是矩形；（2）DG=BE．

Question

正方形ABCD内接于 O，如图所示，在劣弧

AB

上取一点E，连接DE、BE，过点D作DF∥BE交 O于点F，连接BF、AF，且AF与DE相交于点G，求证：

（1）四边形EBFD是矩形；
（2）DG=BE．

Answer 1

证明：（1）∵正方形ABCD内接于 O，
∴∠BED=∠BAD=90°，∠BFD=∠BCD=90°，
又∵DF∥BE，
∴∠EDF+∠BED=180°，
∴∠EDF=90°，
∴四边形EBFD是矩形；

（2））∵正方形ABCD内接于 O，
∴

AD

的度数是90°，
∴∠AFD=45°，
又∵∠GDF=90°，
∴∠DGF=∠DFC=45°，
∴DG=DF，
又∵在矩形EBFD中，BE=DF，
∴BE=DG．