早教吧作业答案频道 -->数学-->
如图,直线y=ax+b与反比例函数y=mx(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.(1)m=,n=;若M(x1,y1),N(x2,y2)是反比例函数
题目详情
如图,直线y=ax+b与反比例函数y=
(x>0)的图象交于A(1,4),B(4,n)两点,与x轴、y轴分别交于C、D两点.
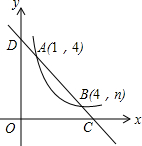
(1)m=___,n=___;若M(x1,y1),N(x2,y2)是反比例函数图象上两点,且0<x1<x2,则y1___y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
| m |
| x |

(1)m=___,n=___;若M(x1,y1),N(x2,y2)是反比例函数图象上两点,且0<x1<x2,则y1___y2(填“<”或“=”或“>”);
(2)若线段CD上的点P到x轴、y轴的距离相等,求点P的坐标.
▼优质解答
答案和解析
(1)∵反比例函数y=
(x>0)的图象过点A(1,4),
∴m=1×4=4.
∵点B(4,n)在反比例函数y=
的图象上,
∴m=4n=4,解得:n=1.
∵在反比例函数y=
(x>0)中,m=4>0,
∴反比例函数y=
的图象单调递减,
∵0<x1<x2,
∴y1>y2.
故答案为:4;1;>.
(2)设过C、D点的直线解析式为y=kx+b,
∵直线CD过点A(1,4)、B(4,1)两点,
∴
,解得:
,
∴直线CD的解析式为y=-x+5.
设点P的坐标为(t,-t+5),
∴|t|=|-t+5|,
解得:t=
.
∴点P的坐标为(
,
).
| m |
| x |
∴m=1×4=4.
∵点B(4,n)在反比例函数y=
| 4 |
| x |
∴m=4n=4,解得:n=1.
∵在反比例函数y=
| 4 |
| x |
∴反比例函数y=
| 4 |
| x |
∵0<x1<x2,
∴y1>y2.
故答案为:4;1;>.
(2)设过C、D点的直线解析式为y=kx+b,
∵直线CD过点A(1,4)、B(4,1)两点,
∴
|
|
∴直线CD的解析式为y=-x+5.
设点P的坐标为(t,-t+5),
∴|t|=|-t+5|,
解得:t=
| 5 |
| 2 |
∴点P的坐标为(
| 5 |
| 2 |
| 5 |
| 2 |
看了 如图,直线y=ax+b与反比...的网友还看了以下:
元素X的核电荷数为a,它的阳离子Xm+与元素Y的阴离子Yn-的电子层结构相同,则元素Y的核电荷数为 2020-05-16 …
若抛物线y=X平方+bX+c与X轴只有一个交点,且过点A(m,n),B(m+6,若抛物线y=X平方 2020-05-17 …
如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB 2020-06-05 …
如图,在△ABC中,AD是∠A的外角平分线,P是AD上异于A的任意一点,设PB=m,PC=n,AB 2020-07-20 …
信息安全数学基础的习题:设m,n为正整数,a>1是整数证明:(a^m-1,a^n-1)=a^(m, 2020-07-22 …
若a,b均为正实数,m,n属于N,且a>b,则a的m次方+b的n次方与a的(m-n)次方b的n次方 2020-07-28 …
很难得数学题设A交集B=∅,m={P|P⊆A},N={Q|Q⊆B},则()A.M∩N=∅B.M∩N 2020-07-30 …
不正确的命题(1816:26:49)1、平面A外两条直线m和n在平面内A的射影分别为m’和n’,给出 2020-11-14 …
设M,N为两个随机事件,如果M,N为互斥事件(.M,.N表示M,N的对立事件),那么()A..M∪. 2020-12-01 …
十万火急,一定重谢!已知A(m,n+1)与B(2m-1,n+3)关于二,四象限夹角平分线对称,求m, 2020-12-19 …