早教吧作业答案频道 -->数学-->
如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.(1)如图2,在△ABC中AB=AC,∠B=50&
题目详情
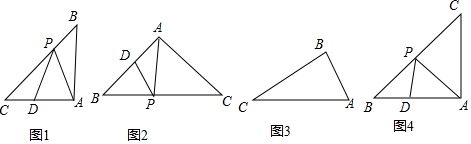
如图1,在△ABC中,在BC边上取一点P,在AC边上取一点D,连AP、PD,如果△APD是等腰三角形且△ABP与△CDP相似,我们称△APD是AC边上的“等腰邻相似三角形”.
(1)如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是___;
(2)如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;
(3)如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”求出AD长度的所有可能值.
(1)如图2,在△ABC中AB=AC,∠B=50°,△APD是AB边上的“等腰邻相似三角形”,且AD=DP,∠PAC=∠BPD,则∠PAC的度数是___;
(2)如图3,在△ABC中,∠A=2∠C,在AC边上至少存在一个“等腰邻相似△APD”,请画出一个AC边上的“等腰邻相似△APD”,并说明理由;
(3)如图4,在Rt△ABC中AB=AC=2,△APD是AB边上的“等腰邻相似三角形”求出AD长度的所有可能值.

▼优质解答
答案和解析
(1)如图2中,
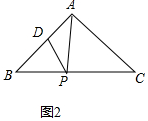
∵AB=AC,DA=DP,
∴∠B=∠C,∠DAP=∠DPA,
∵∠PAC=∠BPD,
∴∠APC=∠BDP=∠DAP+∠DPA,
∵∠APC=∠B+∠BAP,
∴∠B=∠PAB=50°,
∵∠BAC=180°-50°-50°=80°,
∴∠PAC=30°
故答案为30°.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,
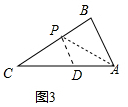
∴∠BAP=∠PAD=∠DPA,∠CPD=∠B,
∵∠CAB=2∠C,
∴∠PAD=∠C,
∴DP=DA,
∴△APD是等腰三角形且与△APB与△CDP相似.
(3)如图3′中,当DA=DP时,设∠APD=∠DAP=x,
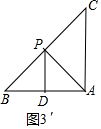
①若∠BPD=∠CAP=90°-x,∠BDP=∠CPA=2x,
∴90°-x+2x+x=180°,
∴x=45°,
∴三角形都是等腰直角三角形,易知AD=1,
②若∠PDB=∠CAP时,设∠APD=∠DAP=x,得到∠PDB=∠CAP=2x,易知x=30°,设AD=a,则AP=
a,
∵△BPD∽△CPA,
∴
=
,即
=
a,解得a=
,
如图4中,当PA=PD时,易知∠PDB是钝角,∠CAP是锐角,
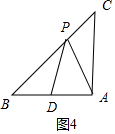
∴∠PDB=∠CPA,则△BPD≌△CPA,设AD=a,则BD=2-a,BP=2
-(2-a),AC=2,
2
-(2-a)=2,
解得a=4-2
,
如图5中,当AP=AD时,设∠APD=∠ADP=x,则∠DAP=180°-2x,易知∠PDB为钝角,∠CAP为锐角,
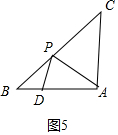
∴∠PDB=∠CAP=180°-x,∠CAP=90°-∠DAP=90°-(180°-2x)=2x-90°,
在△APC中,2x-90°+180°-x+45°=180°,解得x=45°,不可能成立.
综上所述.AD的长为1或
或4-2

∵AB=AC,DA=DP,
∴∠B=∠C,∠DAP=∠DPA,
∵∠PAC=∠BPD,
∴∠APC=∠BDP=∠DAP+∠DPA,
∵∠APC=∠B+∠BAP,
∴∠B=∠PAB=50°,
∵∠BAC=180°-50°-50°=80°,
∴∠PAC=30°
故答案为30°.
(2)如图3中,作∠BAC的平分线AP交BC于P,作PD∥AB交AC于D,

∴∠BAP=∠PAD=∠DPA,∠CPD=∠B,
∵∠CAB=2∠C,
∴∠PAD=∠C,
∴DP=DA,
∴△APD是等腰三角形且与△APB与△CDP相似.
(3)如图3′中,当DA=DP时,设∠APD=∠DAP=x,

①若∠BPD=∠CAP=90°-x,∠BDP=∠CPA=2x,
∴90°-x+2x+x=180°,
∴x=45°,
∴三角形都是等腰直角三角形,易知AD=1,
②若∠PDB=∠CAP时,设∠APD=∠DAP=x,得到∠PDB=∠CAP=2x,易知x=30°,设AD=a,则AP=
| 3 |
∵△BPD∽△CPA,
∴
| BD |
| AC |
| PD |
| PA |
| 2-a |
| 2 |
| a | ||
|
6-2
| ||
| 3 |
如图4中,当PA=PD时,易知∠PDB是钝角,∠CAP是锐角,

∴∠PDB=∠CPA,则△BPD≌△CPA,设AD=a,则BD=2-a,BP=2
| 2 |
2
| 2 |
解得a=4-2
| 2 |
如图5中,当AP=AD时,设∠APD=∠ADP=x,则∠DAP=180°-2x,易知∠PDB为钝角,∠CAP为锐角,

∴∠PDB=∠CAP=180°-x,∠CAP=90°-∠DAP=90°-(180°-2x)=2x-90°,
在△APC中,2x-90°+180°-x+45°=180°,解得x=45°,不可能成立.
综上所述.AD的长为1或
6-2
| ||
| 3 |
作业帮用户
2016-11-21
|
看了 如图1,在△ABC中,在BC...的网友还看了以下:
已知A,B是有理数,且丨AB-2丨与丨B-1丨互为相反数.求AB分之一+【A+1][B+1]分之一 2020-04-05 …
已知一次函数y=(3m-2)x+(m+2)的图像经过点M(3-2a,a+1)上,且3-2a与a+1 2020-05-20 …
与a相邻的两个整数是a-1与a+1这三个数的和是a-1+a+a+1=3a这三个数的平均数是多少?是 2020-05-23 …
若(a+b)(a-1)>0,则必有()(A)b与a同号(B)a+b与a-1同号(C)a>1(D)b 2020-05-24 …
若(a+b)(a-1)>0,则必有()(A)b与a同号(B)a+b与a-1同号(C)a>1(D)b 2020-05-24 …
已知|ab-2|与|a-1|互为相反数求值1/ab+1/(a+1)(b+1)+1/(a+2)(b+ 2020-06-03 …
高一数学已知a^0.5-a^(-0.5)=1(a>0)求a+a^(-1)与a^1.5+a^-1.5 2020-06-03 …
咋做呀,二次函数哦抛物线y=负x的平方加bx加c与x轴交与A(1,0),B(-3,0)两点,(1) 2020-06-04 …
已知|ab-2|与(a-1)*2互为相反数试求1/(a+1)(b+2)+1/(a+3)(b+4)+ 2020-06-06 …
a+1与a-1是同类项吗错了。是a+b与a-b 2020-06-06 …
 扫描下载二维码
扫描下载二维码