早教吧作业答案频道 -->数学-->
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.填空:当点A位于时,线段AC的长取得最大值,且最大值为(用含a,b的式子表示)(2)应用:点A为线段BC外一动点,且BC=3,AB=1,
题目详情
(1)发现:如图1,点A为线段BC外一动点,且BC=a,AB=b.
填空:当点A位于___时,线段AC的长取得最大值,且最大值为___(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.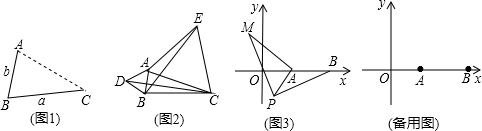
填空:当点A位于___时,线段AC的长取得最大值,且最大值为___(用含a,b的式子表示)
(2)应用:点A为线段BC外一动点,且BC=3,AB=1,如图2所示,分别以AB,AC为边,作等边三角形ABD和等边三角形ACE,连接CD,BE.
①请找出图中与BE相等的线段,并说明理由;
②直接写出线段BE长的最大值.
(3)拓展:如图3,在平面直角坐标系中,点A的坐标为(2,0),点B的坐标为(5,0),点P为线段AB外一动点,且PA=2,PM=PB,∠BPM=90°,请直接写出线段AM长的最大值及此时点P的坐标.

▼优质解答
答案和解析
(1)∵点A为线段BC外一动点,且BC=a,AB=b,
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
,
∴△CAD≌△EAB,
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,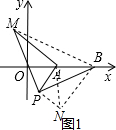
∴最大值为BD+BC=AB+BC=4;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,
∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=
AP=2
,
∴最大值为2
+3;
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=
,
∴OE=BO-
-3=2-
,
∴P(2-
,
).
∴当点A位于CB的延长线上时,线段AC的长取得最大值,且最大值为BC+AB=a+b,
故答案为:CB的延长线上,a+b;
(2)①CD=BE,
理由:∵△ABD与△ACE是等边三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即∠CAD=∠EAB,
在△CAD与△EAB中,
|
∴△CAD≌△EAB,
∴CD=BE;
②∵线段BE长的最大值=线段CD的最大值,
由(1)知,当线段CD的长取得最大值时,点D在CB的延长线上,

∴最大值为BD+BC=AB+BC=4;
(3)连接BM,将△APM绕着点P顺时针旋转90°得到△PBN,连接AN,
则△APN是等腰直角三角形,
∴PN=PA=2,BN=AM,
∵A的坐标为(2,0),点B的坐标为(5,0),
∴OA=2,OB=5,
∴AB=3,

∴线段AM长的最大值=线段BN长的最大值,
∴当N在线段BA的延长线时,线段BN取得最大值,
最大值=AB+AN,
∵AN=
| 2 |
| 2 |
∴最大值为2
| 2 |
如图2,过P作PE⊥x轴于E,
∵△APN是等腰直角三角形,
∴PE=AE=
| 2 |
∴OE=BO-
| 2 |
| 2 |
∴P(2-
| 2 |
| 2 |
看了 (1)发现:如图1,点A为线...的网友还看了以下:
已知:实数a,b,c在数轴上的位置如图所示,且,a的绝对值=b的绝对值.化简:a的绝对值+a和b的 2020-04-05 …
已知实数a,b,c在数轴上的位置如图所示,且绝对值a=绝对值b化简绝对值a加绝对值a加b-根号c- 2020-04-06 …
如何教会孩子拼读孩子学拼音不会拼读,比如b和a,在拼读时会拼成ta,la,fa等,急死了, 2020-05-16 …
如果ax+b=0,其中a,b为有理数,x为无理数,那么a=0且b=0.(1)如果(a-2)2+b+ 2020-06-14 …
如何求两个复合函数的最值例如,b=√(a×a-6a+10)+√(a×a-2a+10)求b的最小值 2020-06-14 …
如何证明均值定理?均值定理:已知x,y∈R+,x+y=S,x·y=P(1)如果P是定值,那么当且仅 2020-06-16 …
③2b=a+c是数列a、b、c为等差数列的充要条件;③2b=a+c是数列a、b、c为等差数列的充要 2020-06-23 …
初一数学难题榜1.如果|a|=4,|b|=3,且a大于b求a和b的值.2如果a初一数学难题榜1.如 2020-07-07 …
证明:如果函数f(x)在[a,b]上可导,且(f(x)导数的绝对值)小于等于M,则,[(f(b)- 2020-07-16 …
有如下算法描述①输入整数a②如果a是奇数转到⑥③如果a是偶数转到⑤④将a的值相乘以后赋给a⑤将a的 2020-07-24 …