早教吧作业答案频道 -->数学-->
上午8时，一条船从海岛A出发，以15nmile/h（海里/时，1nmile=1852m）的速度向正北航行，10时到达海岛B处，从A、B望灯塔C，测得NAC=42°，NBC=84°．则从海岛B到灯塔C的距离为（）
题目详情
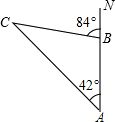上午8时，一条船从海岛A出发，以15n mile/h（海里/时，1n mile=1852m）的速度向正北航行，10时到达海岛B处，从A、B望灯塔C，测得NAC=42°，NBC=84°．则从海岛B到灯塔C的距离为（ ）| A、45n mile |
| B、30n mile |
| C、20n mile |
| D、15n mile |
▼优质解答
答案和解析
考点：
等腰三角形的判定与性质 方向角
专题：
应用题
分析：
根据三角形外角的性质，求证∠C=∠NAC，然后即可证明BC=AB，从而求得B到C的距离．
∵∠NBC=84°，∠NAC=42°，∴∠C=84°-42°=42°．∴∠C=∠NAC，∴BC=AB，∵上午8时，一条船从海岛A出发，以150n mile/h的速度向正北航行．10时到达海岛B处，∴BC=AB=15×2=30n mile．故选B．
点评：
此题考查了等腰三角形的判定和性质，灵活运用等腰三角形性质是解题的关键．
考点：
等腰三角形的判定与性质 方向角
专题：
应用题
分析：
根据三角形外角的性质，求证∠C=∠NAC，然后即可证明BC=AB，从而求得B到C的距离．
∵∠NBC=84°，∠NAC=42°，∴∠C=84°-42°=42°．∴∠C=∠NAC，∴BC=AB，∵上午8时，一条船从海岛A出发，以150n mile/h的速度向正北航行．10时到达海岛B处，∴BC=AB=15×2=30n mile．故选B．
点评：
此题考查了等腰三角形的判定和性质，灵活运用等腰三角形性质是解题的关键．
看了 上午8时，一条船从海岛A出发...的网友还看了以下：