某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝，其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切，上、下桥斜面的坡度i＝1：3.7，桥下水深OP

Question

某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝，其半圆形桥洞的横截面如图所示 . 已知上、下桥的坡面线 ME 、 NF 与半圆相切，上、下桥斜面的坡度 i ＝ 1 ： 3.7 ，桥下水深 OP ＝ 5 米，水面宽度 CD ＝ 24 米 . 设半圆的圆心为 O ，直径 AB 在直角顶点 M 、 N 的连线上，求从 M 点上坡、过桥、下坡到 N 点的最短路径长 . （参考数据： ， ， ）

Answer 1

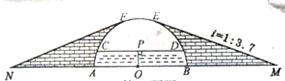
  连结 OD 、 OE 、 OF ，由垂径定理知： PD ＝ 1 2 CD ＝ 12 （ m ） 

在 Rt△OPD 中， （ m ），

∴OE ＝ OD ＝ 13m

∵tan∠EMO=i= 1 ： 3.7 ， ≈ 1 ： 3.7
∴∠EMO ＝ 15°

由切线性质知 ∠OEM ＝ 90°

∴∠EOM=75°
同理得 ∠NOF ＝ 75°

∴∠EOF ＝ 180°-75°×2 ＝ 30°
在 Rt△OEM 中， tan15° ＝

∴EM ＝ 3.7×13 ＝ 48.1 （ m ）

又 EF 的弧长＝ 30π×13÷180 ＝ 6.5 （ m ）

∴48.1×2+6.5 ＝ 102.7 （ m ）

即从 M 点上坡、过桥、再下坡到 N 点的最短路径长为 102.7 米 .