北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积．设隙积共n层，上底由长为a个物体，宽为b个物体组成，以下

Question

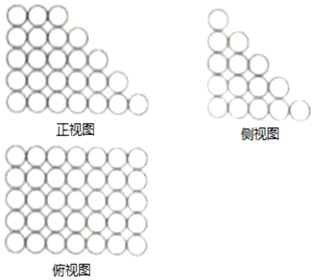
北宋数学家沈括的主要数学成就之一为隙积术，所谓隙积，即“积之有隙”者，如累棋、层坛之类，这种长方台形状的物体垛积．设隙积共n层，上底由长为a个物体，宽为b个物体组成，以下各层的长、宽依次各增加一个物体，最下层成为长为c个物体，宽为d个物体组成，沈括给出求隙积中物体总数的公式为S= (n)/(6)[(2b+d)a+(b+2d)c]+ (n)/(6)(c-a)．已知由若干个相同小球粘黏组成的几何体垛积的三视图如图所示，则该垛积中所有小球的个数为___．

Answer 1

由题意，a=3，b=1，c=7，d=5，n=5，
∴S=(n)/(6)[（2b+d）a+（b+2d）c]+(n)/(6)（c-a）=(5)/(6)[3×（2+5）+7×（1+10）]+(5)/(6)（7-3）=85，
故答案为：85．