如图，E为正方形ABCD内一点，且∠BEC=90°，将△BEC绕B点旋转90°使BC与AB重合，得到△ABF，连EF交AB于P．已知BC=5，AF=4，则AP：BC的值为（）A、3：5B、4：7C、3：4D

Question

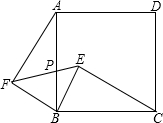如图，E为正方形ABCD内一点，且∠BEC=90°，将△BEC绕B点旋转90°使BC与AB重合，得到△ABF，连EF交AB于P．已知BC=5，AF=4，则AP：BC的值为（　　）

A、3：5

B、4：7

C、3：4

D、5：7

Answer 1

分析：
可证明∠BCE=∠ABE，由∠BCE=∠BAF，得∠BAF=∠ABE，从而得出AF∥BE，△APF∽△BPE，则APBP=AFBE=43，即可得出AP：BC的值．

根据题意得，△ABF∽△CBE，∴∠BCE=∠BAF，∵∠BCE+∠CBE=∠ABE+∠CBE=90°，∴∠BCE=∠ABE，∴∠BAF=∠ABE，∴AF∥BE，∴△APF∽△BPE，∴APBP=AFBE，∵BC=5，AF=4，∴CE=4，∴BE=3，∴APBP=AFBE=43，∴AP：BC=4：7．故选B．
点评：
本题考查了相似三角形的判定和性质、勾股定理、正方形的性质以及旋转的性质，注意旋转前后两个三角形全等．