早教吧作业答案频道 -->数学-->
如图,△ABC内接于O,AC为O的直径,PB是O的切线,B为切点,OP⊥BC,垂足为E,交O于D,连接BD.(1)求证:BD平分∠PBC;(2)若O的半径为1,PD=3DE,求OE及AB的长.
题目详情
如图,△ABC内接于 O,AC为 O的直径,PB是 O的切线,B为切点,OP⊥BC,垂足为E,交 O于D,连接BD.
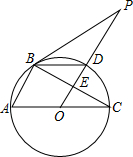
(1)求证:BD平分∠PBC;
(2)若 O的半径为1,PD=3DE,求OE及AB的长.

(1)求证:BD平分∠PBC;
(2)若 O的半径为1,PD=3DE,求OE及AB的长.
▼优质解答
答案和解析
(1)证明:连接OB.
∵PB是 O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.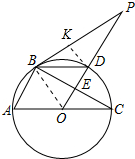
(2) 作DK⊥PB于K,
∵
=
=
,
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴
=
=
,
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴
=
,
∴
=
=
,
∵BO=1,
∴OE=
,
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=
.
∵PB是 O切线,
∴OB⊥PB,
∴∠PBO=90°,
∴∠PBD+∠OBD=90°,
∵OB=OD,
∴∠OBD=∠ODB,
∵OP⊥BC,
∴∠BED=90°,
∴∠DBE+∠BDE=90°,
∴∠PBD=∠EBD,
∴BD平分∠PBC.

(2) 作DK⊥PB于K,
∵
| S△BDE |
| S△BDP |
| ||
|
| DE |
| DP |
∵BD平分∠PBE,DE⊥BE,DK⊥PB,
∴DK=DE,
∴
| BE |
| PB |
| ED |
| PD |
| 1 |
| 3 |
∵∠OBE+∠PBE=90°,∠PBE+∠P=90°,
∴∠OBE=∠P,∵∠OEB=∠BEP=90°,
∴△BEO∽△PEB,
∴
| BO |
| PB |
| OE |
| BE |
∴
| OE |
| BO |
| BE |
| PB |
| 1 |
| 3 |
∵BO=1,
∴OE=
| 1 |
| 3 |
∵OE⊥BC,
∴BE=EC,∵AO=OC,
∴AB=2OE=
| 2 |
| 3 |
看了 如图,△ABC内接于O,AC...的网友还看了以下:
1.PT切圆O于T,CT为直径,D为OC上的一点,支线PD交圆O于B和A,B在线段PD上,若CD= 2020-04-12 …
O.A的英文全称(急) 2020-04-27 …
在三棱柱ABO-A'B'O'中,∠AOB=90,侧棱OO'⊥面OAB,OA=OB=OO'=2.若C 2020-05-12 …
The boy went to the ball,( ) like a pretty girlA. 2020-05-16 …
直角坐标系中A(4,2)O为坐标原点,在x轴上另有一点B,如果以O,A,B为顶点的三角形是等腰三角 2020-05-16 …
平面内有两个定点O(0,0)A(2,0)设点M到O的距离为d1,到A的距离为d2,且d1/d2=根 2020-05-17 …
EXecl表格的一列中值为A的为B的为C的怎么用函数把它们加一起求和 2020-05-17 …
已知点A在单位圆上,且x轴正半轴绕原点逆时针旋转到过A点时所转的最小正角为θ,则向量O→A的坐标为 2020-05-21 …
Thetwogirlsareyournewclassmates,Help,please.A.the 2020-05-22 …
ABO溶血多发生于下列哪种血型情况A.母为O型,婴儿为A或B型B.母为A型,婴儿为O型C.母为O型, 2020-06-04 …