早教吧作业答案频道 -->数学-->
如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.(1)求证:DE•AB=BC•AE;(2)求证:∠AED+∠ADC=180°.
题目详情
如图,点E是四边形ABCD的对角线BD上的一点,∠BAE=∠CBD=∠DAC.
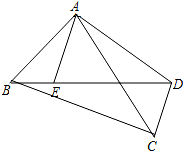
(1)求证:DE•AB=BC•AE;
(2)求证:∠AED+∠ADC=180°.

(1)求证:DE•AB=BC•AE;
(2)求证:∠AED+∠ADC=180°.
▼优质解答
答案和解析
证明:(1)∵∠BAE=∠DAC,
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠EAD,
∵∠ABC=∠ABE+∠CBD,
∠AED=∠ABE+∠BAE,
∵∠CBD=∠BAE,
∴∠ABC=∠AED,
∴△ABC∽△AED,
∴
=
,
∴DE•AB=BC•AE;
(2)∵△ABC∽△AED,
∴
=
,即
=
,
∵∠BAE=∠DAC
∴△ABE∽△ACD,
∴∠AEB=∠ADC,
∵∠AED+∠AEB=180°,
∴∠AED+∠ADC=180°.
∴∠BAE+∠EAC=∠DAC+∠EAC,
即∠BAC=∠EAD,
∵∠ABC=∠ABE+∠CBD,
∠AED=∠ABE+∠BAE,
∵∠CBD=∠BAE,
∴∠ABC=∠AED,
∴△ABC∽△AED,
∴
| AB |
| AE |
| BC |
| DE |
∴DE•AB=BC•AE;
(2)∵△ABC∽△AED,
∴
| AB |
| AE |
| AC |
| AD |
| AB |
| AC |
| AE |
| AD |
∵∠BAE=∠DAC
∴△ABE∽△ACD,
∴∠AEB=∠ADC,
∵∠AED+∠AEB=180°,
∴∠AED+∠ADC=180°.
看了 如图,点E是四边形ABCD的...的网友还看了以下:
A→B表示A是B的同学,且有A→B,B→C那么,A→C一定正确吗?请说明理由 2020-04-26 …
A、B、C、D、E、F六种元素,其中ABCDE为短周期元素,①原子半径A<C<B<E<D②原子最外 2020-05-13 …
一次函数y=x十5的图象经过点P(a,b)在第一象限和点Q(c,d)在第二象限,则a(c一d)一b 2020-05-14 …
已知a+b+c=H a+b+e=J a+d+e=K b+c+d=M c+d+e=N 求a=?b=? 2020-05-16 …
有A,B,C,D,E五中物质,在常温下A,B,C是气体有A、B、C、D、E五种物质,在常温下A、B 2020-05-20 …
给定关系模式R(A,B,C,D)和关系S(A,C,D,E),对其进行自然连接运算,后的属性列为( ) 2020-05-26 …
填空A:()this()English?B:()ajacket.A:()itplease.B:J- 2020-06-06 …
你能辨别下列各组字,并用这个字组成一个成语吗?(1)A.戍B.戌C.戎E.戒A.B.C.E.(2) 2020-06-26 …
设一数列a,b,c,d,e,f,通过栈结构不可能不可能排成的顺序数列为()A)c,b,e,f,d, 2020-06-28 …
小明使用如图所示的abc三根镍络合金丝(a,c一样粗,b,c一样长)进行探究电阻丝的电阻大小跟什因 2020-07-11 …