早教吧作业答案频道 -->数学-->
数学老师布置了这样一道作业题:在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.小聪提供了研究这个问题的过程和思路:先从
题目详情
数学老师布置了这样一道作业题:
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.
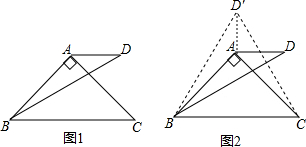
(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决数学老师布置的这道作业题;
(3)解决完老师布置的这道作业题后,小聪进一步思考,当点D和点A在直线BC的异侧时,且∠ADB的度数与(1)中相同,则α,β满足的条件为___(直接写出结果).
在△ABC中,AB=AC≠BC,点D和点A在直线BC的同侧,BD=BC,∠BAC=α,∠DBC=β,α+β=120°,连接AD,求∠ADB的度数.
小聪提供了研究这个问题的过程和思路:先从特殊问题开始研究,当α=90°,β=30°时(如图1),利用轴对称知识,以AB为对称轴构造△ABD的轴对称图形△ABD′,连接CD′(如图2),然后利用α=90°,β=30°以及等边三角形的相关知识便可解决这个问题.

(1)请结合小聪研究问题的过程和思路,求出这种特殊情况下∠ADB的度数;
(2)结合小聪研究特殊问题的启发,请解决数学老师布置的这道作业题;
(3)解决完老师布置的这道作业题后,小聪进一步思考,当点D和点A在直线BC的异侧时,且∠ADB的度数与(1)中相同,则α,β满足的条件为___(直接写出结果).
▼优质解答
答案和解析
(1)如图1
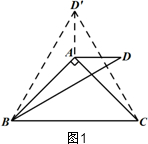
作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=15°,
∵AB=AB,∠AB D′=∠ABD,B D′=BD,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
∵AB=AC,AD'=AD',
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
∠BD′C=30°,
∴∠ADB=30°,
(2) 第一种情况:当60°<α≤120°时,
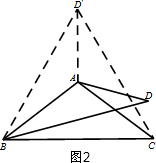
如图2,作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
=90°-
,
∴∠ABD=∠ABC-∠DBC=90°-
-β,
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
-β,BD=BD′,∠ADB=∠AD′B
∴∠D′BC=∠ABD′+∠ABC=90°-
-β+90°-
=180°-(α+β),
∵α+β=120°,
∴∠D′BC=60°,
以下同(1)可求得∠ADB=30°,
第二种情况:当0°<α<60°时,
如图3,
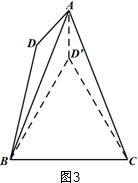
作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′.同理可得:∠ABC=
=90°-
,
∴∠ABD=∠DBC-∠ABC=β-(90°-
),
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β-(90°-
),BD=BD′,∠ADB=∠AD′B,
∴∠D′BC=∠ABC-∠ABD′=90°-
-[β-(90°-
)]=180°-(α+β),
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
(3)点D和点A在直线BC的异侧时,分三种情况讨论:
第一种情况:如图4,
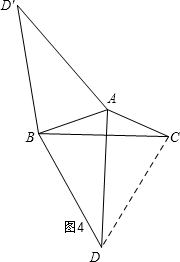
当120°<α<180°,β=60°时,连接CD,
∵∠DBC=β=60°,BD=BC,
∴△DBC是等边三角形,
∴BD=CD,
∴△ABD≌△ACD,
∴∠ADB=∠ADC=30°,
第二种情况:如图5,
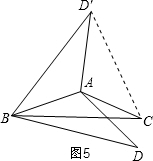
当120°<α<180°,0<β<60°时,连接CD′,
∠ABC=
=90°-
,
∠ABD=∠ABC+∠DBC=90°-
+β,
∵△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
+β,
∵∠ADB=∠AD′B=30°,
∴∠BD′C=60°,
∵BD′=CD′,
∴△BD′C是等边三角形,
∴∠CBD′=(90°-
+β)+(90°-
)=60°,
∴α-β=120°,
第三种情况:如图6,
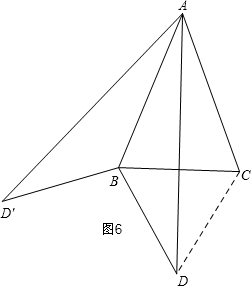
当0°<α<120°,β=60°时,连接CD,
与图4同理得:∠ADB=∠ADC=30°,
故答案为:0°<α<120°,β=60°或120°<α<180°,0<β<60°时,α-β=120°或120°<α<180°,β=60°.

作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,∠BAC=90°,
∴∠ABC=45°,
∵∠DBC=30°,
∴∠ABD=∠ABC-∠DBC=15°,
∵AB=AB,∠AB D′=∠ABD,B D′=BD,
∴△ABD≌△ABD′,
∴∠ABD=∠ABD′=15°,∠ADB=∠AD′B,
∴∠D′BC=∠ABD′+∠ABC=60°,
∵BD=BD′,BD=BC,
∴BD′=BC,
∴△D′BC是等边三角形,
∴D′B=D′C,∠BD′C=60°,
∵AB=AC,AD'=AD',
∴△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∴∠AD′B=
| 1 |
| 2 |
∴∠ADB=30°,
(2) 第一种情况:当60°<α≤120°时,

如图2,作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠BAC=α,
∴∠ABC=
| 180°-α |
| 2 |
| α |
| 2 |
∴∠ABD=∠ABC-∠DBC=90°-
| α |
| 2 |
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
| α |
| 2 |
∴∠D′BC=∠ABD′+∠ABC=90°-
| α |
| 2 |
| α |
| 2 |
∵α+β=120°,
∴∠D′BC=60°,
以下同(1)可求得∠ADB=30°,
第二种情况:当0°<α<60°时,
如图3,

作∠AB D′=∠ABD,B D′=BD,连接CD′,AD′.同理可得:∠ABC=
| 180°-α |
| 2 |
| α |
| 2 |
∴∠ABD=∠DBC-∠ABC=β-(90°-
| α |
| 2 |
同(1)可证△ABD≌△ABD′,
∴∠ABD=∠ABD′=β-(90°-
| α |
| 2 |
∴∠D′BC=∠ABC-∠ABD′=90°-
| α |
| 2 |
| α |
| 2 |
∴D′B=D′C,∠BD′C=60°.
同(1)可证△AD′B≌△AD′C,
∴∠AD′B=∠AD′C,
∵∠AD′B+∠AD′C+∠BD′C=360°,
∴∠ADB=∠AD′B=150°,
(3)点D和点A在直线BC的异侧时,分三种情况讨论:
第一种情况:如图4,

当120°<α<180°,β=60°时,连接CD,
∵∠DBC=β=60°,BD=BC,
∴△DBC是等边三角形,
∴BD=CD,
∴△ABD≌△ACD,
∴∠ADB=∠ADC=30°,
第二种情况:如图5,

当120°<α<180°,0<β<60°时,连接CD′,
∠ABC=
| 180°-α |
| 2 |
| α |
| 2 |
∠ABD=∠ABC+∠DBC=90°-
| α |
| 2 |
∵△ABD≌△ABD′,
∴∠ABD=∠ABD′=90°-
| α |
| 2 |
∵∠ADB=∠AD′B=30°,
∴∠BD′C=60°,
∵BD′=CD′,
∴△BD′C是等边三角形,
∴∠CBD′=(90°-
| α |
| 2 |
| α |
| 2 |
∴α-β=120°,
第三种情况:如图6,

当0°<α<120°,β=60°时,连接CD,
与图4同理得:∠ADB=∠ADC=30°,
故答案为:0°<α<120°,β=60°或120°<α<180°,0<β<60°时,α-β=120°或120°<α<180°,β=60°.
看了 数学老师布置了这样一道作业题...的网友还看了以下:
一次函数的一道题我市A,B两村产柑橘,A有200吨,B产300吨,先将运到C,D两个仓库,已知C可 2020-06-03 …
··一道简单的数学题,先到的.对的.角D=90度,BD=CD,BO是角DBC的角平分线,CE垂直B 2020-06-03 …
设某机器有四个中断源A、B、C、D,其硬件排队优先次序为A>B>C>D,现要求将中断处理次序改为D 2020-06-11 …
鲁迅先生说,侮辱现在,就等到于屠杀现在,而杀了现在,便也杀了将来。其中蕴涵的哲学道理是A.不要侮辱 2020-06-20 …
美国南北战争前,南北矛盾的焦点是A.向西部扩张领土问题B.奴隶制的存废问题C.D.资本主义存废问题 2020-07-13 …
儿童心理学和儿童语言的答案3.从问题的性质来看,可以将问题分为.A.B.归纳结构问题C.D.4.道德 2020-11-21 …
那长方体的最短路径呢?我们来看一下这题(如图)从A′到C,不经过A′B′C′D′和ABCD两面,怎样 2020-11-26 …
美国内战爆发前,南北双方两种经济制度的矛盾发展到了不可调和的地步,其中最尖锐的问题是A.B.奴隶制的 2020-12-28 …
下列属于考试技巧的是()A.时间紧迫,拿到试题先把难题攻克B.做题前认真审题C.做题时先易后难,不着 2020-12-29 …
求解一大学英语单选题Arecentwasthatabout20percentofcollegegra 2021-01-01 …