早教吧作业答案频道 -->数学-->
在Rt△ABC中,∠ACB=90°,∠ABC=45°,点E在线段BC上,射线ED⊥AB于点D.(1)如图1,点F在线段DE上,过F作MN∥BC,M分别交AB、AC于点M、N,点G在线段AF上,且∠GFN=∠GNF,∠GDF=∠GFD.①试判断DG与NG
题目详情
在Rt△ABC中,∠ACB=90°,∠ABC=45°,点E在线段BC上,射线ED⊥AB于点D.
(1)如图1,点F在线段DE上,过F作MN∥BC,M分别交AB、AC于点M、N,点G在线段AF上,且∠GFN=∠GNF,∠GDF=∠GFD.
①试判断DG与NG有怎样的位置关系?直接写出你的结论;
②求证:∠1=∠2;
(2)如图2,点F在线段ED的延长线上,过F作FN∥BC,M,N分别交AB、AC于点M、N,点G在线段AF上,且∠GFN=∠GNF,∠GDF=∠GFD.试探究DG与NG的位置关系,并说明理由.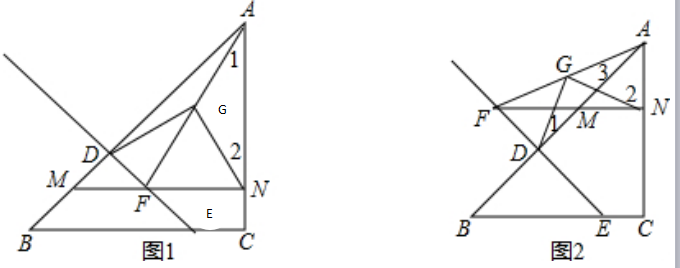
(1)如图1,点F在线段DE上,过F作MN∥BC,M分别交AB、AC于点M、N,点G在线段AF上,且∠GFN=∠GNF,∠GDF=∠GFD.
①试判断DG与NG有怎样的位置关系?直接写出你的结论;
②求证:∠1=∠2;
(2)如图2,点F在线段ED的延长线上,过F作FN∥BC,M,N分别交AB、AC于点M、N,点G在线段AF上,且∠GFN=∠GNF,∠GDF=∠GFD.试探究DG与NG的位置关系,并说明理由.

▼优质解答
答案和解析
(1)①∵MN∥BC,
∴∠ANM=∠ACB=90°,即:∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠1=90°,
∵∠GFN=∠GNF
∴∠1=∠2.
同理可得,∠DAG=∠ADG,
∴∠2+∠ADG=∠BAC=45°,
∵DE⊥AB,
∴∠ADF=90°,
∴∠GDF+∠GNM=180°-45°=135°.
∵∠ACB=90°,∠ABC=45°,DE⊥AB,
∴∠BED=45°,
∴∠DEC=135°.
∵MN∥BC,
∴∠DFN=135°,
∴∠DGN=360°-135°-135°=90°,即DG⊥NG.
②∵MN∥BC,
∴∠ANM=∠ACB=90°,即:∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠1=90°,
∵∠GFN=∠GNF
∴∠1=∠2.
(2)DG⊥GN.
理由如下:
∵FN∥BC,
∴∠ANF=∠ACB=90°,即∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠FAN=90°,
∵∠GFN=∠GNF
∴∠FAN=∠2.
又∵ED⊥AB于D,
∴∠ADF=90°,即:∠GDF+∠1=90°.
在Rt△AFD中,∠GFD+∠3=90°,
∵∠GDF=∠GFD,
∴∠1=∠3.
在△AGD中,∠FGD=∠1+∠3=2∠3.
在△AGN中,∠FGN=∠FAN+∠2=2∠FAN
∴∠NGD=∠FGN-∠FGD
=2∠FAN-2∠3
=2(∠FAN-∠3)
=2∠BAC.
在Rt△ABC中,∠ABC=45°,
∴∠BAC=45°.
∴∠NGD=2∠BAC=90°,
∴DG⊥GN.
∴∠ANM=∠ACB=90°,即:∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠1=90°,
∵∠GFN=∠GNF
∴∠1=∠2.
同理可得,∠DAG=∠ADG,
∴∠2+∠ADG=∠BAC=45°,
∵DE⊥AB,
∴∠ADF=90°,
∴∠GDF+∠GNM=180°-45°=135°.
∵∠ACB=90°,∠ABC=45°,DE⊥AB,
∴∠BED=45°,
∴∠DEC=135°.
∵MN∥BC,
∴∠DFN=135°,
∴∠DGN=360°-135°-135°=90°,即DG⊥NG.
②∵MN∥BC,
∴∠ANM=∠ACB=90°,即:∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠1=90°,
∵∠GFN=∠GNF
∴∠1=∠2.
(2)DG⊥GN.
理由如下:
∵FN∥BC,
∴∠ANF=∠ACB=90°,即∠GNF+∠2=90°.
在Rt△AFN中,∠GFN+∠FAN=90°,
∵∠GFN=∠GNF
∴∠FAN=∠2.
又∵ED⊥AB于D,
∴∠ADF=90°,即:∠GDF+∠1=90°.
在Rt△AFD中,∠GFD+∠3=90°,
∵∠GDF=∠GFD,
∴∠1=∠3.
在△AGD中,∠FGD=∠1+∠3=2∠3.
在△AGN中,∠FGN=∠FAN+∠2=2∠FAN
∴∠NGD=∠FGN-∠FGD
=2∠FAN-2∠3
=2(∠FAN-∠3)
=2∠BAC.
在Rt△ABC中,∠ABC=45°,
∴∠BAC=45°.
∴∠NGD=2∠BAC=90°,
∴DG⊥GN.
看了 在Rt△ABC中,∠ACB=...的网友还看了以下:
如图所示是A-F六种物质之间相互转化关系图.已知B为紫红色固体单质,E为碱,F为蓝色絮状沉淀.(1 2020-04-11 …
已知指数函数y=g(x)满足:g(2)=4,定义域为R上的函数f(x)=−g(x)+ng(x)+m 2020-05-02 …
已知函数f(x)是定义域在(-∞,0)∪(0,+∞)上的不恒为零的函数,且对于任意非零实数a,b满 2020-05-13 …
函数的间断点问题啊不是连续的函数中的跳跃间断点要f(x-)与f(x+)都存在,且f(x-)≠f(x 2020-06-06 …
数学三角定义R在上的偶函数f(x)满足f(x+2)=f(x),且在{-3,-2}上是减函数,若@, 2020-07-02 …
定义在[-1,1]上的奇函数f(x),对任意m、n∈[-1,1],且m+n≠0时,恒有f(m)+f 2020-07-09 …
1.已知f(x)是定义在R上的函数,设g(x)=[f(x)+f(-x)]/2,h(x)=[f(x) 2020-07-19 …
已知,如图1,AB⊥BD于B,ED⊥BD于D,点C在直线BD上且与F重合,AB=FD,BC=DE(1 2020-11-03 …
例题:求函数f(X)=1/(x-1)的间断点,并指出其类型x=1为函数f(X)间断点,因为lim(x 2020-11-28 …
可导函数的导函数未必连续,是不是与左右导数存在且相等的条件矛盾?设f(x)在(a,b)可导,如果f' 2021-02-13 …