早教吧作业答案频道 -->数学-->
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=()A、40°B、45°C、50°D、55°
题目详情
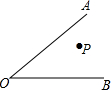 如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )| A、40° | B、45° |
| C、50° | D、55° |
▼优质解答
答案和解析
考点:
轴对称-最短路线问题
专题:
分析:
作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP 1 M=∠OPM=50°,OP 1 =OP 2 =OP,根据等腰三角形的性质即可求解.
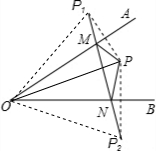 作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,连接P 1 O、P 2 O,
作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,连接P 1 O、P 2 O,
∵PP 1 关于OA对称,
∴∠P 1 OP=2∠MOP,OP 1 =OP,P 1 M=PM,∠OP 1 M=∠OPM=50°
同理,∠P 2 OP=2∠NOP,OP=OP 2 ,
∴∠P 1 OP 2 =∠P 1 OP+∠P 2 OP=2(∠MOP+∠NOP)=2∠AOB,OP 1 =OP 2 =OP,
∴△P 1 OP 2 是等腰三角形.
∴∠OP 2 N=∠OP 1 M=50°,
∴∠P 1 OP 2 =180°-2×50°=80°,
∴∠AOB=40°,
故选A.
点评:
本题考查了对称的性质,正确作出图形,证得△P 1 OP 2 是等腰三角形是解题的关键.
考点:
轴对称-最短路线问题
专题:
分析:
作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,根据对称的性质可以证得:∠OP 1 M=∠OPM=50°,OP 1 =OP 2 =OP,根据等腰三角形的性质即可求解.
 作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,连接P 1 O、P 2 O,
作P关于OA,OB的对称点P 1 ,P 2 .连接OP 1 ,OP 2 .则当M,N是P 1 P 2 与OA,OB的交点时,△PMN的周长最短,连接P 1 O、P 2 O,∵PP 1 关于OA对称,
∴∠P 1 OP=2∠MOP,OP 1 =OP,P 1 M=PM,∠OP 1 M=∠OPM=50°
同理,∠P 2 OP=2∠NOP,OP=OP 2 ,
∴∠P 1 OP 2 =∠P 1 OP+∠P 2 OP=2(∠MOP+∠NOP)=2∠AOB,OP 1 =OP 2 =OP,
∴△P 1 OP 2 是等腰三角形.
∴∠OP 2 N=∠OP 1 M=50°,
∴∠P 1 OP 2 =180°-2×50°=80°,
∴∠AOB=40°,
故选A.
点评:
本题考查了对称的性质,正确作出图形,证得△P 1 OP 2 是等腰三角形是解题的关键.
看了 如图,P为∠AOB内一定点,...的网友还看了以下:
1.PT切圆O于T,CT为直径,D为OC上的一点,支线PD交圆O于B和A,B在线段PD上,若CD= 2020-04-12 …
如图,点P是O上任意一点,O的弦AB所在的直线与P相切于点C,PF为O的直径,设O与P的半径分别为 2020-05-13 …
如图,圆O是三角形ABC的外接圆,点I是三角形ABC的内心如图,AB是圆o的直径,AM和BN是圆o 2020-05-14 …
∵EM是⊙O的切线,怎么推出EB•EC=EM2①?,看题后回答.(2005•温州)如图,已知四边形 2020-05-21 …
关于神经突触的一些问题(关于简图)像“——o>——”这样的,是“——o”为突触前膜,还是“>——” 2020-05-23 …
方程:三个数的和是108,甲数的4倍等于乙数的5倍,甲数比丙数少10,问三个数...方程:三个数的 2020-06-03 …
如图1,AB是O的直径,E是AB延长线上一点,EC切O于点C,OP⊥AO交AC于点P,交EC的延长 2020-06-13 …
我一直搞不明白共振结构是怎么回事.比如说NO2-的一个结构式是O=N-O,它的共振结构的另一个结构 2020-06-16 …
△o-☆=4☆-o△=8△×o×☆=210(☆-o)×(☆△)=希望你们能看得懂.我需要一个解题的 2020-07-09 …
如图所示,三个小球从同一高度处的O点分别以水平初速度v1、v2、v3抛出,落在水平面上的位置分别是 2020-07-21 …