早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形()A、2个B、3个C、4个D、5个
题目详情
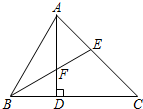 如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )
如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的角平分线BE交AD于点F,则图中共有等腰三角形( )| A、2个 | B、3个 | C、4个 | D、5个 |
▼优质解答
答案和解析
考点:
等腰三角形的判定
专题:
分析:
根据在△ABC中,∠ABC=60°,∠ACB=45°,利用三角形内角和定理求得∠BAC=75°,然后可得等腰三角形.
(1)∵∠ABC=60°,∠ACB=45°,AD是高,∴∠DAC=45°,∴CD=AD,∴△ADC为等腰直角三角形,∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-60°-90°=30°,∴∠ABF=∠BAD=30°,∴AF=BF即△ABF是等腰三角形,在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-60°-45°=75°,∵∠AEB=∠CBE+∠ACB=30°+45°=75°,∴∠BAE=∠BEA,∴AB=EB即△ABE是等腰三角形,∴等腰三角形有△ACD,△ABF,△ABE;故选B.
点评:
本题考查了三角形的内角和定理以及三角形的高、角平分线,等腰三角形的判定、等边三角形的判定,是基础知识要熟练掌握.
考点:
等腰三角形的判定
专题:
分析:
根据在△ABC中,∠ABC=60°,∠ACB=45°,利用三角形内角和定理求得∠BAC=75°,然后可得等腰三角形.
(1)∵∠ABC=60°,∠ACB=45°,AD是高,∴∠DAC=45°,∴CD=AD,∴△ADC为等腰直角三角形,∵∠ABC=60°,BE是∠ABC平分线,∴∠ABE=∠CBE=30°,在△ABD中,∠BAD=180°-∠ABD-∠ADB=180°-60°-90°=30°,∴∠ABF=∠BAD=30°,∴AF=BF即△ABF是等腰三角形,在△ABC中,∠BAC=180°-∠ABC-∠ACB=180°-60°-45°=75°,∵∠AEB=∠CBE+∠ACB=30°+45°=75°,∴∠BAE=∠BEA,∴AB=EB即△ABE是等腰三角形,∴等腰三角形有△ACD,△ABF,△ABE;故选B.
点评:
本题考查了三角形的内角和定理以及三角形的高、角平分线,等腰三角形的判定、等边三角形的判定,是基础知识要熟练掌握.
看了 如图,在△ABC中,∠ABC...的网友还看了以下:
a=-2,b=1时,a的平方-2ab+b的平方分之a的平方-b的平方除以b-a分之a的平方+b的平 2020-04-06 …
当a=-2,b=1时,求a²-2ab+b²分之a²-b²除以b-a分之a²+b²+2ab的值这个题 2020-04-06 …
初一下分式的加减法1.a-b分之a+2b+b-a分之b-a-b分之2a2.xy分之x²+xy-xy 2020-05-13 …
化简a- b分之一1 ÷b- a分之1a- b分之一1 的a是不在分母上的.第二个也是 2020-05-16 …
a=b分之1-c分之1,则c=A.b分之1+abB.b-a分之1C.b+a分之1D.b/1-ab 2020-05-17 …
a+b分之a-b除以b-a分之1乘a-b分之1RT, 2020-06-03 …
关于算术平方数与几何平方数的题目⒊如题谢谢了设a大于0,b大于0,则下列不等式中不正确的一个是?A 2020-06-13 …
已知a>b>c求证a-b分之一加b-a分之一加a-c分之一大于0已知a>b>c求证:a-b分之一加 2020-07-14 …
1.当x=时,分式x+1分之x平方-1的值为02.计算:a-b分之a+b-a分之b=3.方程x分之 2020-07-18 …
a+b分之1,a的平方-b的平方分之2a,b-a分之b的最简公分母是 2020-07-20 …