早教吧作业答案频道 -->数学-->
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);(2)在图A中,取AE的中
题目详情
如图,△ABC中,∠ABC=60°,点E在边BC上,且EA=EB.
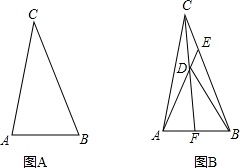
(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);
(2)在图A中,取AE的中点D,若AD=CE,连接CD并延长交AB于点F,请先画出图形,再求∠CFA的度数;
(3)若∠ABC的大小不变,改变∠CAB的大小,得到图B,将(2)中“点D是AE的中点”改为“点D是AE上一点”,其他条件不变,猜想∠CFA与∠DBC的关系,并证明.

(1)请先利用尺规作图的方法找到点E,在图A中标出(保留作图痕迹),在判断此时△ABC的形状(直接写出答案);
(2)在图A中,取AE的中点D,若AD=CE,连接CD并延长交AB于点F,请先画出图形,再求∠CFA的度数;
(3)若∠ABC的大小不变,改变∠CAB的大小,得到图B,将(2)中“点D是AE的中点”改为“点D是AE上一点”,其他条件不变,猜想∠CFA与∠DBC的关系,并证明.
▼优质解答
答案和解析
(1)如图A,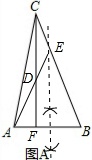
△AEC为等边三角形;
(2)如图A,∵AD=DE,AD=CE,
∴DE=CE,
∴∠ECD=∠EDC,
而∠AEB=∠ECD+∠EDC=60°,
∴∠ECD=30°,
∴∠CFA=∠B+∠BCF=60°+30°=90°;
(3)∠CFA-∠DBC=60°.理由如下:
作DM∥BC交AB于M,如图B,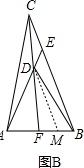
∵△ABE是等边三角形,
∴∠AMD=60°,AD=DM=AM,
∴∴△DAM是等边三角形,
∴∠DEC=∠BMD=120°,
∵DE=AE-AD,BM=AB-AM,
∴DE=BM,
在△DBM和△CDE中,
,
∴△DBM≌△CDE,
∴∠BDM=∠ECD,
∵DM∥BC,
∴∠BDM=∠CBD,
∴∠CBD=∠BCF,
∵∠CFA=∠ABC+∠BCF=60°+∠BCF,
∴∠CFA=60°+∠DBC,
即∠CFA-∠DBC=60°.

△AEC为等边三角形;
(2)如图A,∵AD=DE,AD=CE,
∴DE=CE,
∴∠ECD=∠EDC,
而∠AEB=∠ECD+∠EDC=60°,
∴∠ECD=30°,
∴∠CFA=∠B+∠BCF=60°+30°=90°;
(3)∠CFA-∠DBC=60°.理由如下:
作DM∥BC交AB于M,如图B,

∵△ABE是等边三角形,
∴∠AMD=60°,AD=DM=AM,
∴∴△DAM是等边三角形,
∴∠DEC=∠BMD=120°,
∵DE=AE-AD,BM=AB-AM,
∴DE=BM,
在△DBM和△CDE中,
|
∴△DBM≌△CDE,
∴∠BDM=∠ECD,
∵DM∥BC,
∴∠BDM=∠CBD,
∴∠CBD=∠BCF,
∵∠CFA=∠ABC+∠BCF=60°+∠BCF,
∴∠CFA=60°+∠DBC,
即∠CFA-∠DBC=60°.
看了 如图,△ABC中,∠ABC=...的网友还看了以下:
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0).分别过点A,点B作x轴的垂线,交抛物 2020-05-14 …
··一道简单的数学题,先到的.对的.角D=90度,BD=CD,BO是角DBC的角平分线,CE垂直B 2020-06-03 …
在平面直角坐标系中,若把函数y=x的图像用E(x,x)记,函数y=3x+2的图像用E(x,3x+2 2020-06-06 …
如图,已知直线AB交两坐标于A、B两点,且OA=OB=1,点P(a、b)是双曲线y=12x上在第一 2020-06-11 …
已知:如图,直线AB与直线BC相交于点B,点D是直线BC上一点.求作:点E,使直线DE∥AB,且点 2020-06-15 …
已知,如图,直线AB与直线BC相交于点B,点D是直线BC上一点,求作:点E,使直线DE∥AB,且点 2020-06-22 …
数学圆锥曲线 直线与椭圆 已知椭圆x^2/a^2+y^2/b^2=1(a>b>0)的左右焦点分别为 2020-06-27 …
有A、B、C、D、E、F六个同学比身高.结果是:B比A高11厘米,C比D矮1厘米,E比B高2厘米, 2020-07-07 …
如图,点O是原点,AB∥x轴,点M在线段AB上,且OM=2b,点E是线段AO的中点,若点B和点E关 2020-07-24 …
八年级函数与几何图形的综合应用在直角坐标系中,点B的坐标为(0,根号3),A点在x轴正半轴,E是线 2020-08-02 …