早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.(1)依题意补全图1;(2)判断AE与BD的数量关系与位置关系并加以证明;(3)若0°<
题目详情
如图,在△ABC中,∠ACB=90°,AC=BC=CD,∠ACD=α,将线段CD绕点C顺时针旋转90°得到线段CE,连接DE,AE,BD.
(1)依题意补全图1;
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果).

(1)依题意补全图1;
(2)判断AE与BD的数量关系与位置关系并加以证明;
(3)若0°<α≤64°,AB=4,AE与BD相交于点G,求点G到直线AB的距离的最大值.请写出求解的思路(可以不写出计算结果).
▼优质解答
答案和解析
(1)补全图形,如图1所示.
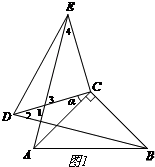
(2)AE与BD的数量关系:AE=BD,
AE与BD的位置关系:AE⊥BD.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB+α=∠DCE+α.
即∠BCD=∠ACE.
∵BC=AC,CD=BC,
∴△BCD≌△ACE.
∴AE=BD.
∴∠4=∠CBD.
∵∠CBD=∠2,
∴∠2=∠4.
∵∠3+∠4=90°,∠1=∠3,
∴∠1+∠2=90°.
即AE⊥BD.
(3)如图2,
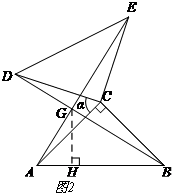
过点G作GH⊥AB于H.
由线段CD的运动可知,当α=64°时GH的长度最大.
∵CB=CD,
∴∠CBD=∠CDB,
∴∠CBD=
=13°,
∴∠DBA=32°.
由(2)可知,∠AGB=90°,
∴∠GAB=58°,
在Rt△GAH中,tan∠GAB=tan58°=
,
∴AH=
,
和Rt△GBH中,tan∠DBA=tan32°=
,
∴BH=
,
∵AB=4,
∴AH+BH=4,
∴
+
=3,
∴GH=3(tan58°+tan32°).

(2)AE与BD的数量关系:AE=BD,
AE与BD的位置关系:AE⊥BD.
证明:∵∠ACB=∠DCE=90°,
∴∠ACB+α=∠DCE+α.
即∠BCD=∠ACE.
∵BC=AC,CD=BC,
∴△BCD≌△ACE.
∴AE=BD.
∴∠4=∠CBD.
∵∠CBD=∠2,
∴∠2=∠4.
∵∠3+∠4=90°,∠1=∠3,
∴∠1+∠2=90°.
即AE⊥BD.
(3)如图2,

过点G作GH⊥AB于H.
由线段CD的运动可知,当α=64°时GH的长度最大.
∵CB=CD,
∴∠CBD=∠CDB,
∴∠CBD=
| 180°-90°-64° |
| 2 |
∴∠DBA=32°.
由(2)可知,∠AGB=90°,
∴∠GAB=58°,
在Rt△GAH中,tan∠GAB=tan58°=
| GH |
| AH |
∴AH=
| GH |
| tan58° |
和Rt△GBH中,tan∠DBA=tan32°=
| GH |
| BH |
∴BH=
| GH |
| tan32° |
∵AB=4,
∴AH+BH=4,
∴
| GH |
| tan58° |
| GH |
| tan32° |
∴GH=3(tan58°+tan32°).
看了 如图,在△ABC中,∠ACB...的网友还看了以下:
(2014•滨湖区二模)如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,A 2020-04-07 …
如图,四边形ABCD是直角梯形,其中,AE=EB=CD=3厘米,BC=ED=2厘米.以CD边为轴, 2020-05-13 …
如图,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么P 2020-05-24 …
如图,正方形ABCD的边长为3,以CD为一边向CD两侧作等边三角形PCD和等边三角形QCD,那么P 2020-05-24 …
如图所示,在直线AB上有7个点,直线CD上有9个点.以AB上的点为一个端点、CD上的点为另一个端点 2020-06-15 …
如图为桥洞的形状,其正视图是由CD和矩形ABCD构成.O点为CD所在O的圆心,点O又恰好在AB为水 2020-07-10 …
如图,C、D是以AB为直径的⊙O上的两个动点(点C、D与点A、B不重合),在运动过程中弦CD长始终 2020-07-11 …
如图,定长弦CD在以AB为直径的⊙O上滑动(点C、D与点A、B不重合),M是CD的中点,过点D作D 2020-07-30 …
如图,AB⊥BD,CD⊥BD,∠A+∠AEF=180°.求证:CD//EF.证明:因为AB⊥BD,C 2020-11-02 …
(2008•邵阳)如图,AB、CD是竖立在公路两侧,且架设了跨过公路的高压电线的电杆,AB=CD=1 2020-11-12 …