早教吧作业答案频道 -->数学-->
如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;(1)如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由
题目详情
如图1,在Rt△ACB中,∠BAC=90°,AB=AC,分别过B、C两点作过点A的直线l的垂线,垂足为D、E;
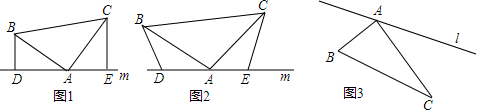
(1)如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出结果即可)

(1)如图1,当D、E两点在直线BC的同侧时,猜想,BD、CE、DE三条线段有怎样的数量关系?并说明理由.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)如图3,∠BAC=90°,AB=22,AC=28.点P从B点出发沿B→A→C路径向终点C运动;点Q从C点出发沿C→A→B路径向终点B运动.点P和Q分别以每秒2和3个单位的速度同时开始运动,只要有一点到达相应的终点时两点同时停止运动;在运动过程中,分别过P和Q作PF⊥l于F,QG⊥l于G.问:点P运动多少秒时,△PFA与△QAG全等?(直接写出结果即可)
▼优质解答
答案和解析
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)①当0≤t<
时,点P在AB上,点Q在AC上,
此时有BF=2t,CG=3t,AB=22,AC=28.
当PA=QA即22-2t=28-3t,也即t=6时,
∵PF⊥l,QG⊥l,∠BAC=90°,
∴∠PFA=∠QGA=∠BAC=90°.
∴∠PAF=90°-∠GAQ=∠AQG.
在△PFA和△QAG中,
,
∴PFA与≌QAG(AAS).
②当
≤t<11时,点P在AB上,点Q也在AB上,
此时相当于两点相遇,则有2t+3t=50,解得t=10;
③当7<t<18时,点Q停在点B处,点P在AC上,
当PA=QA即2t-22=22,解得t=22(舍去).
综上所述:当t等于6或10时,△PFA与△QAG全等.
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠CAE=∠ABD,
在△ADB和△CEA中,
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)①当0≤t<
| 28 |
| 3 |
此时有BF=2t,CG=3t,AB=22,AC=28.
当PA=QA即22-2t=28-3t,也即t=6时,
∵PF⊥l,QG⊥l,∠BAC=90°,
∴∠PFA=∠QGA=∠BAC=90°.
∴∠PAF=90°-∠GAQ=∠AQG.
在△PFA和△QAG中,
|
∴PFA与≌QAG(AAS).
②当
| 28 |
| 3 |
此时相当于两点相遇,则有2t+3t=50,解得t=10;
③当7<t<18时,点Q停在点B处,点P在AC上,
当PA=QA即2t-22=22,解得t=22(舍去).
综上所述:当t等于6或10时,△PFA与△QAG全等.
看了 如图1,在Rt△ACB中,∠...的网友还看了以下:
已知函数f(x)=x^3+x-16.直线l为曲线y=f(x)的切线,且经过原点,求直线l的方程及切 2020-05-20 …
已知直线L经过(0,-2)其倾斜角为60度.求直线L的方程?求以(根号3,1)为圆心,与直线L相切 2020-05-21 …
直线l过点(-1,0),圆C的圆心为C(2,0).(Ⅰ)若圆C的半径为2,直线l截圆C所得的弦长也 2020-07-26 …
直线和圆的位置关系:设⊙O的圆心O到直线l的距离为d,⊙O的半径为r(1)直线l和圆O没有公共点⇔ 2020-07-26 …
过点p(3.4)的直线l在y轴上的截距为71求直线l的方程,2求过o(5,0)且和直线l平过点p( 2020-07-30 …
若直线l的参数x=3+4/5t与y=2+3/5t其中t为参数(4,-1)且与直线l平行的直线l'在 2020-07-30 …
倾斜角为α的直线l过点P(8,2),直线l和曲线C:x=42cosθy=2sinθ(θ为参数)交于 2020-08-01 …
已知直线l:y=1/2x-1,l关于直线x-y+3=0对称的直线方程为希望能有具体解题思路和过程!已 2020-10-31 …
一次函数对称型练习题若直线L与直线y=kx+b关于(1)x轴对称,则直线L的解析式为(2)y轴对称, 2020-11-11 …
本题原本就没有图A为直线l上一点,B是直线l上一点,点A到l的距离为3cm,则AB()3cm,根据是 2020-12-13 …