早教吧作业答案频道 -->数学-->
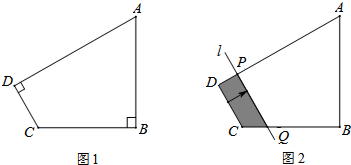
如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=43.(1)求CD边的长;(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q(点Q运动到点B停止).设DP=x,四边形PQCD的面积为y,求
题目详情
如图1,四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=
.
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q(点Q运动到点B停止).设DP=x,四边形PQCD的面积为y,求y与x的函数关系式,并求出自变量x的取值范围.
| 4 |
| 3 |
(1)求CD边的长;
(2)如图2,将直线CD边沿箭头方向平移,交DA于点P,交CB于点Q(点Q运动到点B停止).设DP=x,四边形PQCD的面积为y,求y与x的函数关系式,并求出自变量x的取值范围.

▼优质解答
答案和解析
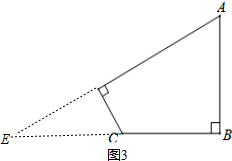 (1)如图(3),分别延长AD、BC相交于E,
(1)如图(3),分别延长AD、BC相交于E,
在Rt△ABE中,
∵tanA=
,AB=3,BC=2,
∴BE=4,EC=2,AE=5,
又∵∠E+∠A=90°,∠E+∠ECD=90°,
∴∠A=∠ECD,
由tanA=
,得cosA=
,
∴cos∠ECD=
=
,
∴CD=
;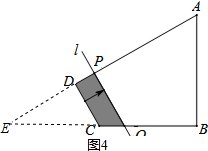
(2)如图4,由(1)可知tan∠ECD=
=
,
∴ED=
,
如图4,由PQ∥DC,可知△EDC~△EPQ,
∴
=
,
∴
=
,即PQ=
+
x,
∵S四边形PQCD=S△EPQ-S△EDC,
∴y=
PQ•EP-
DC•ED=
×(
+
x)×(
+x)-
×
×
=
x2+
x,
∴当Q点到达B点时,点P在M点处,
由EC=BC,DC∥PQ,
∴DM=ED=
,
∴自变量x的取值方范围为:0<x≤
.
 (1)如图(3),分别延长AD、BC相交于E,
(1)如图(3),分别延长AD、BC相交于E,在Rt△ABE中,
∵tanA=
| 4 |
| 3 |
∴BE=4,EC=2,AE=5,
又∵∠E+∠A=90°,∠E+∠ECD=90°,
∴∠A=∠ECD,
由tanA=
| 4 |
| 3 |
| 3 |
| 5 |
∴cos∠ECD=
| CD |
| EC |
| 3 |
| 5 |
∴CD=
| 6 |
| 5 |

(2)如图4,由(1)可知tan∠ECD=
| ED |
| CD |
| 4 |
| 3 |
∴ED=
| 8 |
| 5 |
如图4,由PQ∥DC,可知△EDC~△EPQ,
∴
| ED |
| EP |
| DC |
| PQ |
∴
| ||
|
| ||
| PQ |
| 6 |
| 5 |
| 3 |
| 4 |
∵S四边形PQCD=S△EPQ-S△EDC,
∴y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 6 |
| 5 |
| 3 |
| 4 |
| 8 |
| 5 |
| 1 |
| 2 |
| 6 |
| 5 |
| 8 |
| 5 |
| 3 |
| 8 |
| 6 |
| 5 |
∴当Q点到达B点时,点P在M点处,
由EC=BC,DC∥PQ,
∴DM=ED=
| 8 |
| 5 |
∴自变量x的取值方范围为:0<x≤
| 8 |
| 5 |
看了 如图1,四边形ABCD中,∠...的网友还看了以下:
在三角形ABC中,a,b,c分别为角A,B,C的对边,如果a+c=2b,角B=30度,三角形ABC 2020-04-05 …
分可以加!如图,四边形ABCD为边长是a的正方形,分别以点A、B、C、D如图,四边形ABCD为边长 2020-05-16 …
一个宏观经济学的问题!在一个三部门经济中,税收采用定量税形式,T=T0.如果假设货币需求函数是L= 2020-06-20 …
在三角形ABC中,如果AB边上的高与AB边的长相等,则AC/BC+BC/AC+AB^2/BC*AC 2020-07-22 …
1.等比数列{An}的前n项和为Sn=3的2n-1次方+a,则常数a的值?2.三角形ABC中,a, 2020-07-24 …
在△ABC和△A'B'C'中,已知∠C=∠C'=90°,点D,D'分别在边AB,A'B'上,且CD 2020-07-30 …
在不等边三角形ABC中a为最大边,如果a方小于b方+c方,则A的取值范围 2020-08-03 …
设a、b、c是一个三角形的三边,如果a+b=2c,那么这个三角形一定是()A.等边三角形B.不等边 2020-08-03 …
在不等边三角形ABC中,a为最大边,如果a^2<b^2+c^2,则角A的取值范围是多少 2020-08-03 …
(1)在RT三角形ABC中,角C=90°,a.b.c分别为其三边,c为斜边,若c+a=18,c-a 2020-08-04 …