早教吧作业答案频道 -->数学-->
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:①∠EBG=45°;②
题目详情
如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论:
①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是___.(填写正确结论的序号)
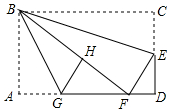
①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是___.(填写正确结论的序号)

▼优质解答
答案和解析
∵根据折叠得出∠BAG=∠FBG,∠CBE=∠FBE,
又∵四边形ABCD是矩形,
∴∠BAC=90°,
∴∠EBG=
×90°=45°,∴①正确;
∵四边形ABCD是矩形,
∴AB=DC=6,BC=AD=10,∠A=∠C=∠D=90°,
∴根据折叠得∠BFE=∠C=90°,
∴∠ABG+∠BGA=90°,∠EFD+∠BFA=90°,
∵∠BGA>∠BFA,
∴∠BAG≠∠EFD,
∵∠GHB=∠A=90°,∠EFB=∠C=90°,
∴∠GHB=∠EFB,
∴GH∥EF,
∴∠EFD=∠HGF,
根据已知不能推出∠AGB=∠HGF,
∴∠AGB≠∠EFD,
即△DEF和△ABG不全等,∴②错误;
∵根据折叠得:AB=BH=6,BC=BF=10,
∴由勾股定理得:AF=
=8,
∴DF=10-8=2,HF=10-6=4,
设AG=HG=x,
在Rt△FGH中,由勾股定理得:GH2+HF2=GF2,
即x2+42=(8-x)2,
解得:x=3,
即AG=HG=3,
∴S△ABG=
×AB×AG=
×6×3=9,S△FHG=
×GH×HF=
×3×4=6,∴③错误;
∵AG+DF=3+2=5,GF=10-3-2=5,∴④正确;
故答案为:①④.
又∵四边形ABCD是矩形,
∴∠BAC=90°,
∴∠EBG=
| 1 |
| 2 |
∵四边形ABCD是矩形,
∴AB=DC=6,BC=AD=10,∠A=∠C=∠D=90°,
∴根据折叠得∠BFE=∠C=90°,
∴∠ABG+∠BGA=90°,∠EFD+∠BFA=90°,
∵∠BGA>∠BFA,
∴∠BAG≠∠EFD,
∵∠GHB=∠A=90°,∠EFB=∠C=90°,
∴∠GHB=∠EFB,
∴GH∥EF,
∴∠EFD=∠HGF,
根据已知不能推出∠AGB=∠HGF,
∴∠AGB≠∠EFD,
即△DEF和△ABG不全等,∴②错误;
∵根据折叠得:AB=BH=6,BC=BF=10,
∴由勾股定理得:AF=
| 102-62 |
∴DF=10-8=2,HF=10-6=4,
设AG=HG=x,
在Rt△FGH中,由勾股定理得:GH2+HF2=GF2,
即x2+42=(8-x)2,
解得:x=3,
即AG=HG=3,
∴S△ABG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵AG+DF=3+2=5,GF=10-3-2=5,∴④正确;
故答案为:①④.
看了 如图,在矩形纸片ABCD中,...的网友还看了以下:
英语翻译O2O即OnlineToOffline(在线离线/线上到线下),是指将线下的商务机会与互联 2020-04-11 …
将带点的内容换成成语,使语句更简洁1.江面上大雾漫天,渔船一会儿看得见,一会儿看不见( ).... 2020-05-16 …
试列一表格,将质点的直线运动(刚体在直线上平动)和刚体定轴转动的运动学规律和动力学规律作一对比. 2020-05-17 …
双曲线的一条准线将两点的焦点的连线分成3:2两段.双曲线的离心率是多少 2020-05-21 …
能不能将带点的词换成括号里的词?如果不能说说为什么不能.一天,贾岛去长安城拜访{访问}一个叫李凝的 2020-05-23 …
一笔共6条线将4点的点阵连起来.................能否用一笔(不能断笔)共6条线将以 2020-06-02 …
地面上某点,相对高程为296.345米,2、地面上某点,测得其相对高程为296.345米,若后来测 2020-06-05 …
将带点的字和恰当的字义用线连起来.举世闻名(举字)动作行为举足轻重(举字)全举一反三(举字)拾一举 2020-06-19 …
在平面直角坐标系中,将线段的两个端点的纵坐标都加上2,横坐标保持不变,所得图形位置与原线段相比(2 2020-06-21 …
在平面直角坐标系中,将线段的两个端点的纵坐标都加上2,横坐标保持不变,所得图形位置与原线段相比 2020-06-21 …