早教吧作业答案频道 -->数学-->
如图,平面直角坐标系中,A(2,0),△OAC为等边三角形.(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM
题目详情
如图,平面直角坐标系中,A(2,0),△OAC为等边三角形.
(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.
(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM为等边三角形,MA的延长线交y轴于N,求AM-AP的值.
(3)如图3,若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F,求证:AF+MF=PF.
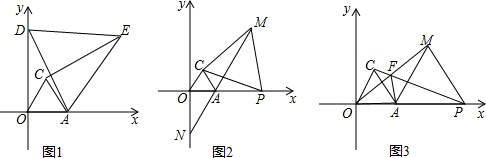
(1)如图1,若D(0,4),△ADE为等边三角形,∠DAC=10°,求∠AEC的度数.
(2)如图2,若P为x轴正半轴上一点,且P在A的右侧,△PCM为等边三角形,MA的延长线交y轴于N,求AM-AP的值.
(3)如图3,若P为x轴正半轴上一点,且P在A的右侧,△PAM为等边三角形,OM与PC交于F,求证:AF+MF=PF.

▼优质解答
答案和解析
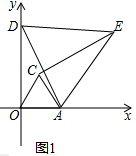 (1) 如图1,∵△AOC和△DAE是等边三角形,
(1) 如图1,∵△AOC和△DAE是等边三角形,
∴AC=AO,AE=AD,∠OAC=∠EAD=60°
∴∠CAE=∠DAO=60○-∠CAD,
在△CAE和△OAD中,
,
∴△CAE≌△OAD(SAS),
∴CE=OD=4,∠ACE=∠AOD=90°,
∵∠DAC=10°,∠DAE=60°,
∴∠CAE=60°+10°=70°,
∴∠AEC=180°-90°-70°=20°;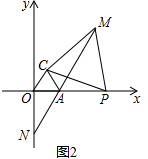
(2) 如图2,∵△AOC和△CPM是等边三角形,
∴OA=AC,CP=CM,∠OCA=∠MCP=60°,
∴∠OCP=∠ACM,
在△OCP和△ACM中,
,
∴△OCP≌△ACM(SAS),
∴AM=OP,
∴AM-OP=OP-AP=OA,
∵A(2,0),
∴OA=2,
即AM-AP=2;
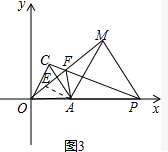
(3)证明:如图3,将△PAF顺时针旋转60°得到△EAM,
则△PAF≌△MAE,∠FAE=60°,
∴PF=EM,AF=AE,
∴△EAF是等边三角形,
∴EF=AF,
∴AF+MF=EF+MF=EM=PF,即AF+MF=PF.
 (1) 如图1,∵△AOC和△DAE是等边三角形,
(1) 如图1,∵△AOC和△DAE是等边三角形,∴AC=AO,AE=AD,∠OAC=∠EAD=60°
∴∠CAE=∠DAO=60○-∠CAD,
在△CAE和△OAD中,
|
∴△CAE≌△OAD(SAS),
∴CE=OD=4,∠ACE=∠AOD=90°,
∵∠DAC=10°,∠DAE=60°,
∴∠CAE=60°+10°=70°,
∴∠AEC=180°-90°-70°=20°;

(2) 如图2,∵△AOC和△CPM是等边三角形,
∴OA=AC,CP=CM,∠OCA=∠MCP=60°,
∴∠OCP=∠ACM,
在△OCP和△ACM中,
|
∴△OCP≌△ACM(SAS),
∴AM=OP,
∴AM-OP=OP-AP=OA,
∵A(2,0),
∴OA=2,
即AM-AP=2;

(3)证明:如图3,将△PAF顺时针旋转60°得到△EAM,
则△PAF≌△MAE,∠FAE=60°,
∴PF=EM,AF=AE,
∴△EAF是等边三角形,
∴EF=AF,
∴AF+MF=EF+MF=EM=PF,即AF+MF=PF.
看了 如图,平面直角坐标系中,A(...的网友还看了以下:
对坐标的曲面积分∫∫(xz)dxdy其中是平面x=0,y=0,z=0,x+y+z=1所围成的空间区 2020-05-16 …
图纸标注H=-0.05.那么H-0.85该降多少图纸总标注为H=-0.05,层高为6.9米,现在版 2020-05-17 …
立面体和平面图的标高数字标注在标高符号()。A.右侧B.左侧C.上侧D.下侧 2020-05-31 …
排列图中左侧纵坐标和右侧纵坐标分别表示质量影响因素出现的( )。A.频率和重要程度 B.频数和重 2020-06-07 …
y=f(|x|)的图像为什么是将y=f(x)的y轴右侧的图像翻折至左侧?y轴左侧x≤0,可是|x| 2020-06-24 …
场地平整后的地面标高-0.5米,基坑底的标高-2.2米,边缘系数m=0.5,已知基础底部尺寸为20 2020-06-24 …
已知四棱锥的底面是矩形,侧棱长相等,棱锥的高为4,其俯视图如图所示.(1)作出此四棱锥的正视图和侧 2020-06-30 …
有一种牙膏侧面的标签如图:(1)单氟磷酸钠的化学式是Na2PO3F,若该牙膏中的含氟量为0.19% 2020-07-29 …
建筑和结构标高相关我现在施工中的图纸,建筑图上标的全是结构标高.现地面结构标高为+0.35.地面做法 2020-11-02 …
如图是鲫鱼的外形图,请按要求回答问题:(1)图中标号③的名称是(2)“鱼儿”离不开水,是因为鱼用呼吸 2020-12-25 …