已知E为正△ABC内任意一点．求证：以AE、BE、CE为边可以构成一个三角形．若∠BEC=113°，∠AEC=123°，求构成三角形的各角度数．

Question

已知E为正△ABC内任意一点．求证：以AE、BE、CE为边可以构成一个三角形．若∠BEC=113°，∠AEC=123°，求构成三角形的各角度数．

Answer 1

证明：①∵△ABC是等边三角形，
∴AB=BC=CA；∠ACB=60°，
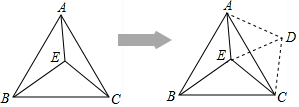
∴将△BEC绕点C逆时针旋转60°，至△ACD，BC与AC重合，连接ED，
∴△ADC≌△AEB，
∴AD=AE，BE=CD，∠EAD=60°，
∴△AED是等边三角形，
∴ED=AE，
∴以AE、BE、CE为边可以构成一个三角形，△CDE即所构三角形；
②∵∠BEC=113°，∠AEC=123°，
∴∠AEB=360°-113°-123°=360°-236°=124°，
由△ADC≌△AEB得：∠ADC=AEB=124°，
∴∠EDC=124°-60°=64°，
∠DEC=123°-60°=63°，
∴∠ECD=180°-64°-63°=53°，
∴构成三角形的各角度数分别为：63°、53°、64°．