早教吧作业答案频道 -->数学-->
如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.(1)如图2、图3,当∠CDF=0°或60°
题目详情
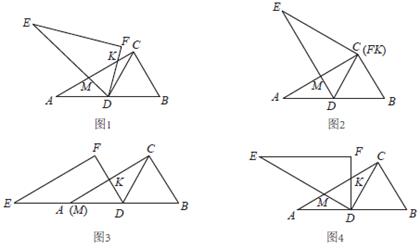
如图1,有两个全等的直角三角形△ABC和△EDF,∠ACB=∠F=90°,∠A=∠E=30°,点D在边AB上,且AD=BD=CD.△EDF绕着点D旋转,边DE,DF分别交边AC于点M,K.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CK___MK(填“>”,“<”或“=”),你的依据是___;
(2)如图4,当∠CDF=30°时,AM+CK___MK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CK___MK,试证明你的猜想.
(1)如图2、图3,当∠CDF=0°或60°时,AM+CK___MK(填“>”,“<”或“=”),你的依据是___;
(2)如图4,当∠CDF=30°时,AM+CK___MK(填“>”或“<”);
(3)猜想:如图1,当0°<∠CDF<60°时,AM+CK___MK,试证明你的猜想.

▼优质解答
答案和解析
(1)在Rt△ABC中,D是AB的中点,
∴AD=BD=CD=
AB,∠B=∠BDC=60°
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;
(2)由(1),得∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30°,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK,
(3)AM+CK>MK,
证明:作点A关于ED的对称点G,连接GK,GM,GD.
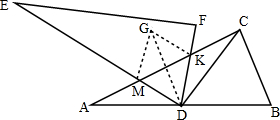
∵点G是点A关于直线DE的对称点
∴AD=GD,GM=AM,∠GDM=∠ADM,
∵Rt△ABC 中,D是AB的中点,
∴AD=CD=GD.
∵∠A=∠E=30°,
∴∠CDA=120°,∠EDF=60°,
∴∠GDM+∠GDK=60°,∠ADM+∠CDK=60°,
∴∠GDK=∠CDK,
在△GDK和△CDK中,
∵
,
∴△GDK≌△CDK(SAS),
∴GK=CK,
∵GM+GK>MK,
∴AM+CK>MK.
∴AD=BD=CD=
| 1 |
| 2 |
又∵∠A=30°,
∴∠ACD=60°-30°=30°,
又∵∠CDE=60°,或∠CDF=60°时,
∴∠CKD=90°,
∴在△CDA中,AM(K)=CM(K),即AM(K)=KM(C)(等腰三角形底边上的垂线与中线重合),
∵CK=0,或AM=0,
∴AM+CK=MK;
(2)由(1),得∠ACD=30°,∠CDB=60°,
又∵∠A=30°,∠CDF=30°,∠EDF=60°,
∴∠ADM=30°,
∴AM=MD,CK=KD,
∴AM+CK=MD+KD,
∴在△MKD中,AM+CK>MK,
(3)AM+CK>MK,
证明:作点A关于ED的对称点G,连接GK,GM,GD.

∵点G是点A关于直线DE的对称点
∴AD=GD,GM=AM,∠GDM=∠ADM,
∵Rt△ABC 中,D是AB的中点,
∴AD=CD=GD.
∵∠A=∠E=30°,
∴∠CDA=120°,∠EDF=60°,
∴∠GDM+∠GDK=60°,∠ADM+∠CDK=60°,
∴∠GDK=∠CDK,
在△GDK和△CDK中,
∵
|
∴△GDK≌△CDK(SAS),
∴GK=CK,
∵GM+GK>MK,
∴AM+CK>MK.
看了 如图1,有两个全等的直角三角...的网友还看了以下:
下列条件中,能做出唯一三角形的是A、已知三个角B、已知两边和其中一边的对角C、已知三角形的周长D、已 2020-03-30 …
下列各条件中,能作出唯一三角形的是A:已知三个角B:已知两边和其中一边的对角C:已知三角形的周长‘D 2020-03-30 …
初中相似三角形证明题在三角形ABC的边上有一点D,角C等于角BAD,求证AD2:AD2等于BD:BC 2020-03-30 …
在四边形abcd中,角a等于90度,角b比角c比角d等于一比二比三,则角b等于多少,角c等于多少,角 2020-03-30 …
在四边形ABCD中,若角A+角B=角C+角D,角C+2角D,则角C=答好追分! 2020-05-01 …
如图,AB、CD相交于点O,EO⊥AB于O,则图中∠1与∠2的关系是()。A.对顶角B.互补的两角 2020-05-14 …
请问这是什么星星.在直角三角形ABC中,A为30度锐角,B为90度直角,C为60度锐角.延长AC到 2020-05-14 …
如图是一块梯形铁片的残余部分,量出∠A=120°,∠B=105°,AB=20cm,并且还知道原来梯 2020-05-23 …
以下()是车轮外倾角的定义。A.转向轴线向前或向后的倾角B.从轮胎顶部测量,轮胎向内或向外的倾角C. 2020-05-31 …
在直角坐标系中,已知点A(-2.0),B(0,4)C(0.3).过C作直线交X轴于D.使以D.O. 2020-06-02 …