早教吧作业答案频道 -->数学-->
如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为217,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.(Ⅰ)证明:GH∥EF;(Ⅱ)若EB=2
题目详情
如图所示,四棱锥P-ABCD的底面是边长为8的正方形,四条侧棱长均为2
,点G,E,F,H分别是棱PB,AB,CD,PC上共面的四点,平面GEFH⊥平面ABCD,BC∥平面GEFH.
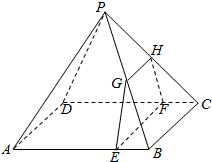
(Ⅰ)证明:GH∥EF;
(Ⅱ)若EB=2,求四棱锥D-GEFH的体积.
| 17 |

(Ⅰ)证明:GH∥EF;
(Ⅱ)若EB=2,求四棱锥D-GEFH的体积.
▼优质解答
答案和解析
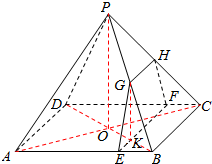 (Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC⊂平面ABCD,
(Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC⊂平面ABCD,
∴BC∥EF,
∵EF⊄平面PBC,BC⊂平面PBC,
∴EF∥平面PBC,
∵平面EFGH∩平面PBC=GH,
∴EF∥GH;
(Ⅱ) 连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
∵PA=PC,O为AC中点,
∴PO⊥AC,
同理可得PO⊥BD,
又∵BD∩AC=O,AC⊂底面ABCD,BD⊂底面ABCD,
∴PO⊥底面ABCD,
又∵平面GEFH⊥平面ABCD,PO⊄平面GEFH,
∴PO∥平面GEFH,
∵平面PBD∩平面GEFH=GK,
∴PO∥GK,且GK⊥底面ABCD
∴GK是梯形GEFH的高
∵AB=8,EB=2,
∴
=
=
,
∴KB=
DB=
OB,即K为OB中点,
又∵PO∥GK,
∴GK=
PO,即G为PB中点,且GH=
BC=4,
由已知可得OB=4
,PO=6,
∴GK=3,
故四边形GEFH的面积S=
(4+8)×3=18
∵D到平面GEFH的距离为6,
∴四棱锥D-GEFH的体积为
×18×6=36.
 (Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC⊂平面ABCD,
(Ⅰ)证明:∵BC∥平面GEFH,平面GEFH∩平面ABCD=EF,BC⊂平面ABCD,∴BC∥EF,
∵EF⊄平面PBC,BC⊂平面PBC,
∴EF∥平面PBC,
∵平面EFGH∩平面PBC=GH,
∴EF∥GH;
(Ⅱ) 连接AC,BD交于点O,BD交EF于点K,连接OP,GK.
∵PA=PC,O为AC中点,
∴PO⊥AC,
同理可得PO⊥BD,
又∵BD∩AC=O,AC⊂底面ABCD,BD⊂底面ABCD,
∴PO⊥底面ABCD,
又∵平面GEFH⊥平面ABCD,PO⊄平面GEFH,
∴PO∥平面GEFH,
∵平面PBD∩平面GEFH=GK,
∴PO∥GK,且GK⊥底面ABCD
∴GK是梯形GEFH的高
∵AB=8,EB=2,
∴
| EB |
| AB |
| KB |
| DB |
| 1 |
| 4 |
∴KB=
| 1 |
| 4 |
| 1 |
| 2 |
又∵PO∥GK,
∴GK=
| 1 |
| 2 |
| 1 |
| 2 |
由已知可得OB=4
| 2 |
∴GK=3,
故四边形GEFH的面积S=
| 1 |
| 2 |
∵D到平面GEFH的距离为6,
∴四棱锥D-GEFH的体积为
| 1 |
| 3 |
看了 如图所示,四棱锥P-ABCD...的网友还看了以下:
把一副三角尺(30°,60°,90°,和45°,45°,90°)如图(甲)放置在平面直角坐标系中, 2020-04-13 …
1/a+1/b+1/c=1/d+1/e+1/f+1/g=1(a,b,c,d,e,f,g均为自然数) 2020-05-13 …
1.已知f(x),g(x)均为R上的奇函数且f(x)>0解集为(4,10),g(x)>0解集为(2 2020-05-14 …
设z=f(x*y)+g(y/x).其中f,g均可微.求x的偏导 2020-05-20 …
一个等效平衡题某温度下密闭容器中发生如下可逆反应2E[g]==F[g]+xG[g]若起始时E的浓度 2020-06-06 …
复合函数奇偶性质的证明对于复合函数F(x)=f[g(x)](1)若g(x)为偶函数,则F(x)为偶 2020-06-08 …
求证确界问题——数分大一问题设f,g均为E上的有界函数:求证inff(E)+infg(E) 2020-06-11 …
为什么由于F,G均为二次连续可微函数,形为u=F(ξ)+G(η)的函数u必满足二阶混合偏导为零? 2020-07-16 …
已知:如图,△ABC中,D,E,F,G均为BC边上的点,且BD=CG,DE=GF=1/2BD,EF 2020-07-20 …
已知Z=xf(y/x)+2yg(x/y),其中f,g均为二阶可导函数,求az/ax,a²z/axay 2020-10-30 …