如图，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，C半径为2，P为圆上一动点，连结AP，BP，则AP+12BP的最小值为（）A.37B.6C.217D.4

Question

如图，在Rt△ABC中，∠ACB=90°，CB=4，CA=6， C半径为2，P为圆上一动点，连结AP，BP，则AP+

(1)/(2)BP的最小值为（　　）

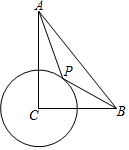
A.

√(37)

B. 6

C. 2 

√(17)

D. 4

Answer 1

如图1，连接CP，在CB上取点D，使CD=1，则有(CD)/(CP)=(CP)/(CB)=(1)/(2)，

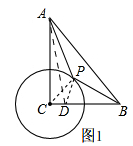
又∵∠PCD=∠BCP，
∴△PCD∽△BCP，
∴(PD)/(BP)=(1)/(2)，
∴PD=(1)/(2)BP，
∴AP+(1)/(2)BP=AP+PD．
要使AP+(1)/(2)BP最小，只要AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，
即：AP+(1)/(2)BP最小值为AD，
在Rt△ACD中，CD=1，AC=6，
∴AD=√(AC2+CD2)=√(37)，
AP+(1)/(2)BP的最小值为√(37)，
故选A．